算法系列题
程序代码使用c++编写,如果对c++基本语法还不熟悉,建议先去了解,这样有助于更快的理解代码。
数组中重复的数字
找出数组中重复的数字
题目:在一个长度为n的数组里的所有数字都在0~n-1的范围内。数组中某些数字是重复的,但不知道有几个数字重复了,也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。例如,如果输入长度为7的数组{2,3,1,0,2,5,3},那么对应的输出是重复的数字2或者3。
传统思路:
- 先排序,再从头到尾扫描,时间复杂度O(nlogn),空间复杂度O(1)
- 使用哈希表,从头到尾扫描,表中不存在则加入,存在则找到该数,时间复杂度O(n),空间复杂度O(n)
新思路:
在数组长度(n)>=数组值的范围(0~n-1)时,说明每个数组值(m)都可以放置到其值对应的数组序号([m] = m)中,所以我们只需从头到尾扫描数组,将每个元素交换到其值对应的序号位置,如果对应的序号位置存在值且为m,那我们就找到了重复的数字。
bool duplicate(int numbers[], int length, int* duplication)
{
if(numbers == nullptr || length <= 0)
return false;
for(int i = 0; i < length; ++i)
{
if(numbers[i] < 0 || numbers[i] > length - 1)
return false;
}
for(int i = 0; i < length; ++i)
{
while(numbers[i] != i) // 注意:这里会一直找到当前序号对应的值
{
if(numbers[i] == numbers[numbers[i]])
{
*duplication = numbers[i];
return true;
}
int temp = numbers[i];
numbers[i] = numbers[temp];
numbers[temp] = temp;
}
}
return false;
}
代码中尽管有一个两重循环,但每个数字最多只要交换两次就能找到属于自己的位置,因此时间复杂度为O(n)。另外,所以的操作步骤都是在输入数组上进行的,不需要额外分配内存,因此,空间复杂度为O(1)。
不修改数组找出重复的数字
题目:在一个长度为n+1的数组里的所有数字都在1~n的范围内,所以数组中至少有一个数字是重复的。请找出数组中任意一个重复的数字,但不能修改输入的数组。例如,如果输入长度为8的数组{2,3,5,4,3,2,6,7},那么对应的输出是重复的数字2或者3。
传统思路:
- 使用哈希表,从头到尾扫描,表中不存在则加入,存在则找到该数,时间复杂度O(n),空间复杂度O(n)
新思路:
假如没有重复的数字,那么在从1~n的范围里只有n个数字。由于数组里包含超过n个数字,所以一定包含里重复的数字。
我们把从1~n的数字从中间的数字m分为两部分,前面一半为1~m,后面一半为m+1~n。如果1~m的数字的数目超过m,那么这一半的区间一定包含重复的数字。否则,另一半m+1~n的区间里一定包含重复的数字。我们可以继续把包含重复数字的区间一分为二,直到找到一个重复的数字。这个过程和二分查找算法很类似,只是多了一步统计区间里数字的数目。
int countRange(const int* numbers, int length, int start, int end);
int getDuplication(const int* numbers, int length)
{
if(numbers == nullptr || length <= 0)
return -1;
int start = 1;
int end = length - 1;
while(end >= start)
{
int middle = ((end - start) >> 1) + start;
int count = countRange(numbers, length, start, middle);
if(end == start)
{
if(count > 1)
return start;
else
break;
}
if(count > (middle - start + 1))
end = middle;
else
start = middle + 1;
}
return -1;
}
int countRange(const int* numbers, int length, int start, int end)
{
if(numbers == nullptr)
return 0;
int count = 0;
for(int i = 0; i < length; i++)
if(numbers[i] >= start && numbers[i] <= end)
++count;
return count;
}
时间复杂度O(nlogn),空间复杂度O(1),和传统思路相比,是以时间换空间。而且这种方法没法保证找出所以重复的数字,因为下面两种情况会都认为区间内不存在重复数字:
- 在一个区间内所有数字都只出现一次
- 在一个区间内有的数字出现多次有的数字没有出现但总个数与区间长度相同
二维数组中的查找
题目:在一个二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
传统思路:
从数组选取一个数字,分3种情况来分析查找。选取数字和查找数字相等,结束查处。如果选取数字小于查找数字,要查找的数字应该在当前选取位置的右边或者下边。同样,如果选取的数字大于要查找的数字,那么要查找的数字应该在选取位置的上边或者左边:
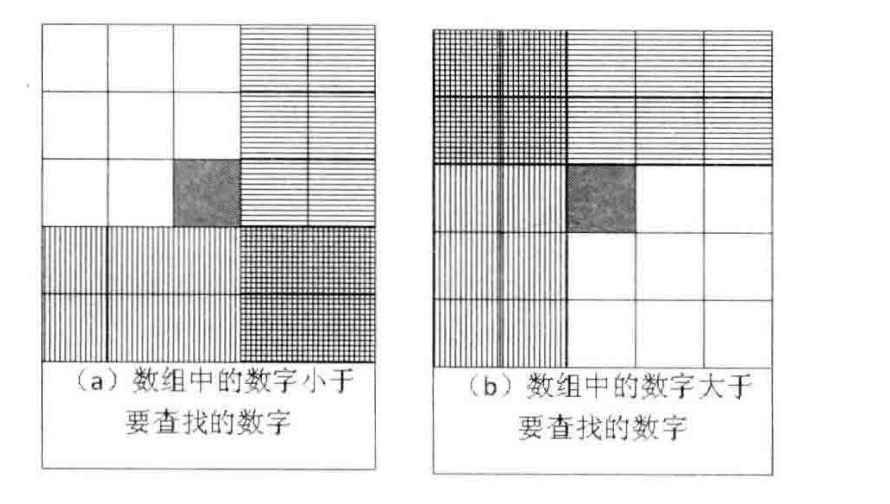
在这种分析中,由于要查找的数字相对于当前选取位置有可能在两个区域中出现,而且这两个区域还有重叠,这问题看起来就复杂了。
新思路:
如果我们从数组的一个角上选取数字来和要查找的数字进行比较,那么情况是不是变简单了呢?我们以选取数组右上角的数字为例,目标数字为7:

我们发现每一步都可以缩小查找范围,直到找到要查找的数字。
bool Find(int* matrix, int rows, int columns, int number)
{
bool found = false;
if(matrix != nullptr && rows > 0 && columns > 0)
{
int row = 0;
int column = columns - 1;
while(row < rows && column >=0)
{
if(matrix[row * columns + column] == number)
{
found = true;
break;
}
else if(matrix[row * columns + column] > number)
-- column;
else
++ row;
}
}
return found;
}
替换空格
题目:请实现一个函数,把字符串中的每个空格替换成”%20”。例如输入“We are happy.”,则输出“We%20are%20happy.”。
传统思路:
这里我们假设我们可以在原来的字符串上进行替换,并保证输入字符串后面有足够多的空余内存。从头到尾扫描字符串,每次碰到空格字符的时候进行替换。由于是把一个字符替换成3个字符,我们必须要把空格后的所以字符都后移2个字节。

时间复杂度是O(n^2)。
新思路:
先遍历一次字符串,统计出空格的总数,并由此计算出替换之后的字符串的总长度。我们从字符串后面开始复制和替换,准备两个指针:P1和P2,P1指向原始字符串的末尾,而P2指向替换之后的字符串的末尾。
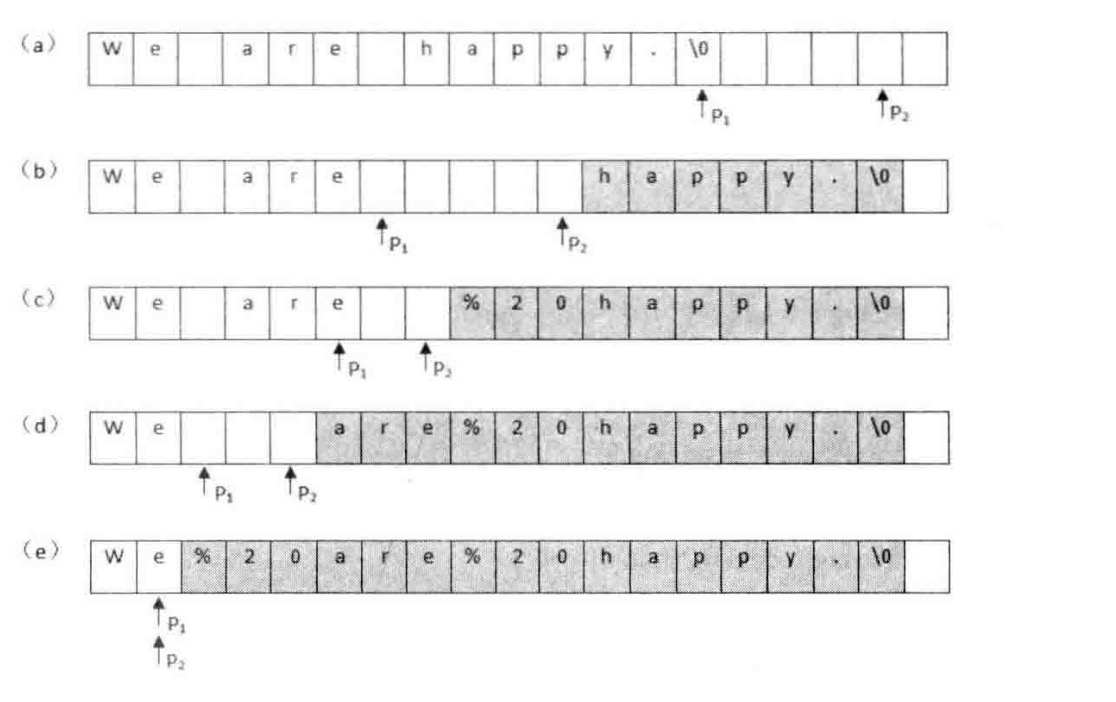
/*length 为字符数组str的总容量,大于或等于字符串str的实际长度*/
void ReplaceBlank(char str[], int length)
{
if(str == nullptr && length <= 0)
return;
/*originalLength 为字符串str的实际长度*/
int originalLength = 0;
int numberOfBlank = 0;
int i = 0;
while(str[i] != '\0')
{
++ originalLength;
if(str[i] == ' ')
++ numberOfBlank;
++ i;
}
/*newLength 为把空格替换成'%20'之后的长度*/
int newLength = originalLength + numberOfBlank * 2;
if(newLength > length)
return;
int indexOfOriginal = originalLength;
int indexOfNew = newLength;
while(indexOfOriginal >= 0 && indexOfNew > indexOfOriginal)
{
if(str[indexOfOriginal] == ' ')
{
str[indexOfNew --] = '0';
str[indexOfNew --] = '2';
str[indexOfNew --] = '%';
}
else
{
str[indexOfNew --] = str[indexOfOriginal];
}
-- indexOfOriginal;
}
}
相关题目:有两个排序的数组A1和A2,内存在A1的末尾有足够多的空余空间容纳A2。请实现一个函数,把A2中的所有数字插入A1中,并且所有的数字是排序的。
和前面的例题一样,我们可以从尾到头比较A1和A2中的数字,并把较大的数字复制到A1中的合适位置。
从尾到头打印链表
题目:输入一个链表的头结点,从尾到头反过来打印出每个结点的值。
struct ListNode
{
int m_nValue;
ListNode* m_pNext;
};
1,将链表中链接节点的指针翻转过来,改变链表的方向,就可以从头到尾输出量。但这会改变原来链表的结构。
2,假设不能改变链表结构,使用栈来实现“后进先出”的顺序:
#include <stack>
void PrintListReversingly_Iteratively(ListNode* pHead)
{
std::stack<ListNode*> nodes;
ListNode* pNode = pHead;
while(pNode != nullptr)
{
nodes.push(pNode);
pNode = pNode->m_pNext;
}
while(!nodes.empty())
{
pNode = nodes.top();
printf("%d\t", pNode->m_nValue);
nodes.pop();
}
}
3,既然想到了用栈来实现,而递归本质上就是一个栈结构,于是很自然又想到用递归来实现。要实现反过来输出链表,我们每访问一个节点时,先递归输出它后面的节点,再输出该节点自身:
void PrintListReversingly_Recursively(ListNode* pHead)
{
if(pHead != nullptr)
{
if (pHead->m_pNext != nullptr)
{
PrintListReversingly_Recursively(pHead->m_pNext);
}
printf("%d\t", pHead->m_nValue);
}
}
递归代码看起来很简洁,但有一个问题:当链表非常长的时候,就会导致函数调用的层级很深,有可能导致函数调用栈溢出。显然用栈基于循环实现的代码鲁棒性要好一些。
重建二叉树
题目:输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2, 4, 7, 3, 5, 6, 8}和中序遍历序列{4, 7, 2, 1, 5, 3, 8, 6},则重建出二叉树并输出它的头结点,如图所示:
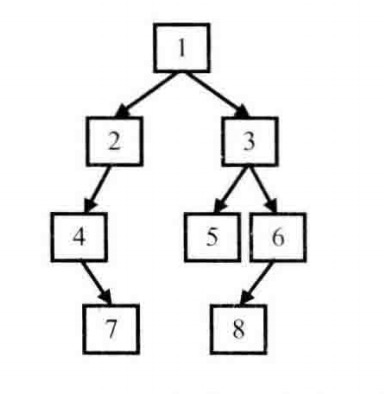
二叉树节点定义如下:
struct BinaryTreeNode
{
int m_nValue;
BinaryTreeNode* m_pLeft;
BinaryTreeNode* m_pRight;
};
二叉树的前序遍历序列中,第一个数字总是树的根结点的值。但在中序遍历序列中,根结点但值在序列的中间,左子树的节点位于根结点的值的左边,而右子树的节点位于根结点的值的右边:
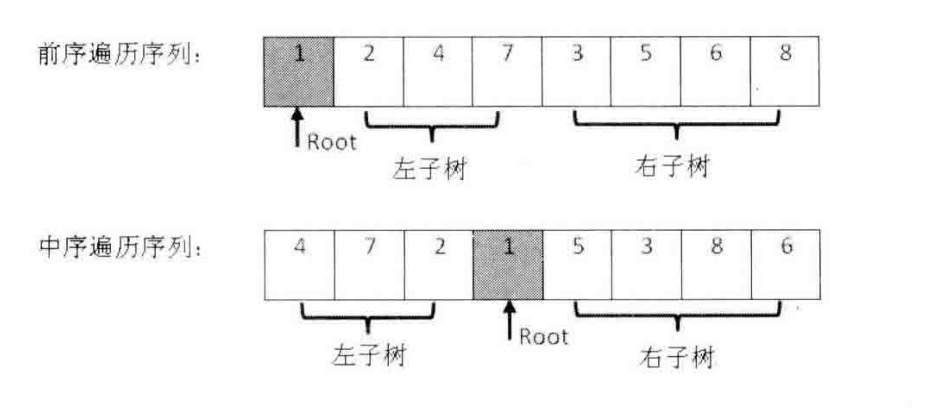
我们可以找到左、右子树的前序遍历序列和中序遍历序列,接着通过递归用同样的方法分别构建左、右子树:
BinaryTreeNode* ConstructCore(int* startPreorder, int* endPreorder, int* startInorder, int* endInorder);
BinaryTreeNode* Construct(int* preorder, int* inorder, int length)
{
if(preorder == nullptr || inorder == nullptr || length <= 0)
return nullptr;
return ConstructCore(preorder, preorder + length - 1,
inorder, inorder + length - 1);
}
BinaryTreeNode* ConstructCore
(
int* startPreorder, int* endPreorder,
int* startInorder, int* endInorder
)
{
// 前序遍历序列的第一个数字是根结点的值
int rootValue = startPreorder[0];
BinaryTreeNode* root = new BinaryTreeNode();
root->m_nValue = rootValue;
root->m_pLeft = root->m_pRight = nullptr;
if(startPreorder == endPreorder)
{
if(startInorder == endInorder && *startPreorder == *startInorder)
return root;
else
throw std::exception("Invalid input.");
}
// 在中序遍历中找到根结点的值
int* rootInorder = startInorder;
while(rootInorder <= endInorder && *rootInorder != rootValue)
++ rootInorder;
if(rootInorder == endInorder && *rootInorder != rootValue)
throw std::exception("Invalid input.");
int leftLength = rootInorder - startInorder;
int* leftPreorderEnd = startPreorder + leftLength;
if(leftLength > 0)
{
// 构建左子树
root->m_pLeft = ConstructCore(startPreorder + 1, leftPreorderEnd,
startInorder, rootInorder - 1);
}
if(leftLength < endPreorder - startPreorder)
{
// 构建右子树
root->m_pRight = ConstructCore(leftPreorderEnd + 1, endPreorder,
rootInorder + 1, endInorder);
}
return root;
}
二叉树的下一个结点
题目:给定一棵二叉树和其中的一个结点,如何找出中序遍历顺序的下一个结点?树中的结点除了有两个分别指向左右子结点的指针以外,还有一个指向父结点的指针。
我们以下图这棵树(中序遍历序列是{d,b,h,e,i,a,f,c,g})来分析如何找出二叉树的下一个节点:
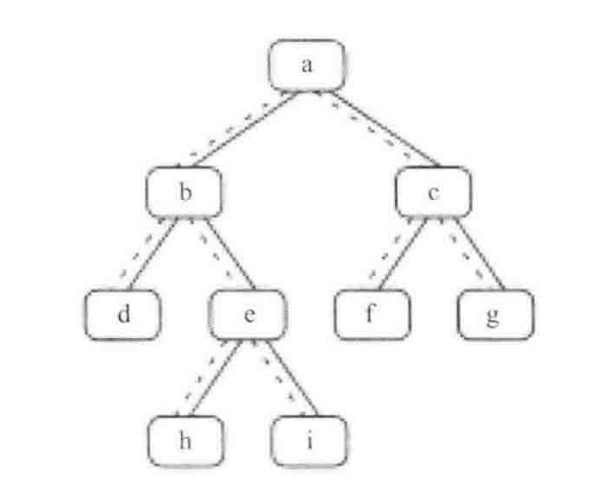
1,如果一个节点有右子树,那么它的下一个节点就是它的右子树中最左子节点。也就是说,从右子节点出发一直沿着指向左子节点的指针,我们就可以找到它的下一个节点。图中节点b的下一个节点是h,节点a的下一个节点是f。
2,接着我们分析一个节点没有右子树的情形。如果节点是它父节点的左子节点,那么它的下一个节点就是它的父节点。图中节点d的下一个节点是b,节点f的下一个节点是c。
3,如果一个节点既没有右子树,并且它还是它父节点的右子节点,那么这种情形就比较复杂。我们可以沿着指向父节点的指针一直向上遍历,直到找到一个是它父节点的左子节点的节点。如果这样的节点存在,那么这个节点就是我们要找的下一个节点。如果不存在,则没有下一个节点。
struct BinaryTreeNode
{
int m_nValue;
BinaryTreeNode* m_pLeft;
BinaryTreeNode* m_pRight;
BinaryTreeNode* m_pParent;
};
BinaryTreeNode* GetNext(BinaryTreeNode* pNode)
{
if(pNode == nullptr)
return nullptr;
BinaryTreeNode* pNext = nullptr;
if(pNode->m_pRight != nullptr)
{
BinaryTreeNode* pRight = pNode->m_pRight;
while(pRight->m_pLeft != nullptr)
pRight = pRight->m_pLeft;
pNext = pRight;
}
else if(pNode->m_pParent != nullptr)
{
BinaryTreeNode* pCurrent = pNode;
BinaryTreeNode* pParent = pNode->m_pParent;
while(pParent != nullptr && pCurrent == pParent->m_pRight)
{
pCurrent = pParent;
pParent = pParent->m_pParent;
}
pNext = pParent;
}
return pNext;
}
用两个栈实现队列
题目:用两个栈实现一个队列。队列的声明如下,请实现它的两个函数appendTail和deleteHead,分别完成在队列尾部插入结点和在队列头部删除结点的功能。
template <typename T> class CQueue
{
public:
CQueue(void);
~CQueue(void);
// 在队列末尾添加一个结点
void appendTail(const T& node);
// 删除队列的头结点
T deleteHead();
private:
stack<T> stack1;
stack<T> stack2;
};
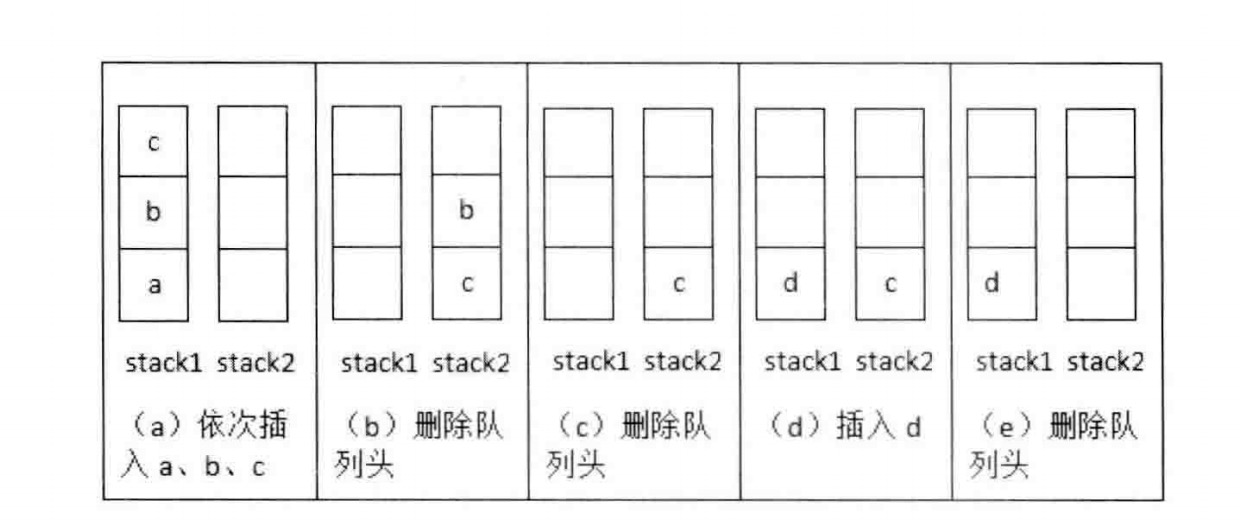
题目意图是要求我们操作这两个“先进后出”的栈实现一个“先进先出”的队列CQueue。难度不高,如图所示:
#pragma once
#include <stack>
#include <exception>
using namespace std;
template <typename T> class CQueue
{
public:
CQueue(void);
~CQueue(void);
// 在队列末尾添加一个结点
void appendTail(const T& node);
// 删除队列的头结点
T deleteHead();
private:
stack<T> stack1;
stack<T> stack2;
};
template <typename T> CQueue<T>::CQueue(void)
{
}
template <typename T> CQueue<T>::~CQueue(void)
{
}
template <typename T> void CQueue<T>::appendTail(const T& element)
{
stack1.push(element);
}
template <typename T> T CQueue<T>::deleteHead()
{
if(stack2.size()<= 0)
{
while(stack1.size()>0)
{
T& data = stack1.top();
stack1.pop();
stack2.push(data);
}
}
if(stack2.size() == 0)
throw new exception("queue is empty");
T head = stack2.top();
stack2.pop();
return head;
}
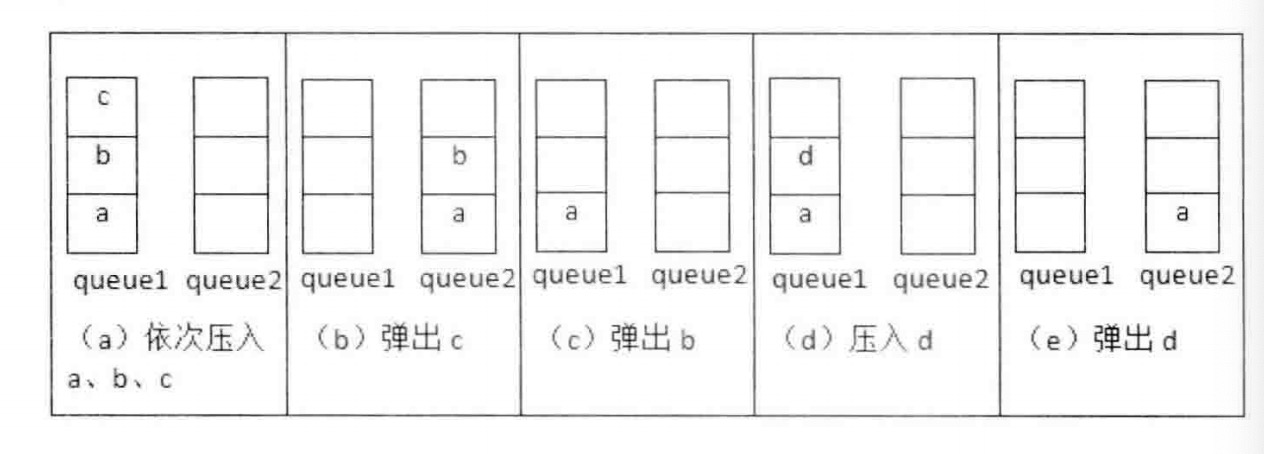
相关题目:用两个队列实现一个栈。
斐波那契数列
题目:写一个函数,输入n,求斐波那契(Fibonacci)数列的第n项。斐波那契数列定义如下:
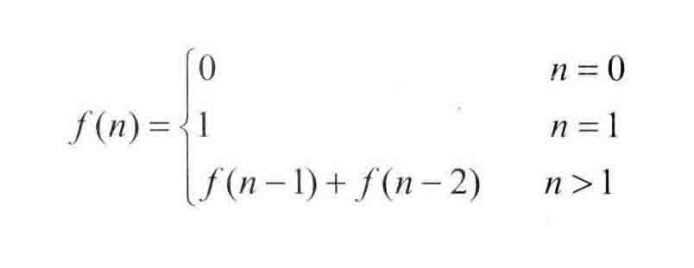
使用递归:
long long Fibonacci_Solution1(unsigned int n)
{
if(n <= 0)
return 0;
if(n == 1)
return 1;
return Fibonacci_Solution1(n - 1) + Fibonacci_Solution1(n - 2);
}
但这种解法有很严重的效率问题,我们以求解f(10)为例来分析递归的求解过程。想求得f(10),需要先求得f(9)和f(8)。同样,想求得f(9),需要先求得f(8)和f(7)…我们可以用树形结构来表示这种依赖关系:
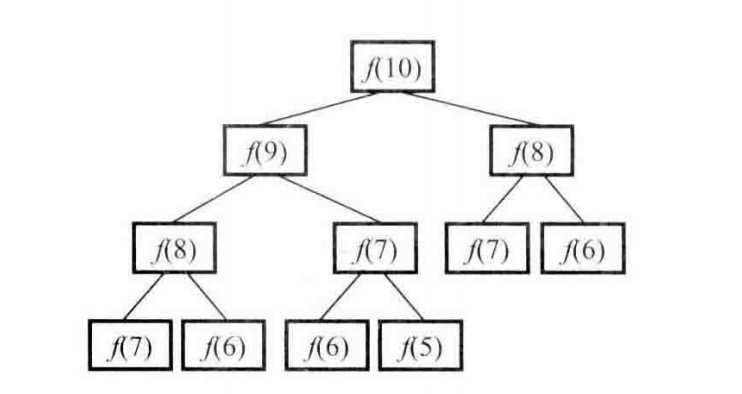
不难发现,这棵树中有很多节点是重复的,而且重复的节点数会随着n的增大而急剧增加,这意味着计算量会随着n的增大而急剧增大。事实上,用递归方法计算的时间复杂度是以n的指数的方式递增的。
使用循环:
其实改进的方法并不复杂,上述递归代码之所以慢,是因为重复的计算太多,我们只要避免重复计算就行了。比如我们可以把已经得到的数列中间项保存起来,在下次需要计算的时候先查找一下,如果前面已经计算过就不再重复计算了。
更简单的办法是从下往上计算,首先根据f(0)和f(1)算出f(2),再根据f(1)和f(2)算出f(3)…以此类推就可以算出第n项了。这种思路的时间复杂度是O(n)。代码如下:
long long Fibonacci_Solution2(unsigned n)
{
int result[2] = {0, 1};
if(n < 2)
return result[n];
long long fibNMinusOne = 1;
long long fibNMinusTwo = 0;
long long fibN = 0;
for(unsigned int i = 2; i <= n; ++ i)
{
fibN = fibNMinusOne + fibNMinusTwo;
fibNMinusTwo = fibNMinusOne;
fibNMinusOne = fibN;
}
return fibN;
}
相关题目:一只青蛙一次可以跳上1级台阶,也可也跳上2级台阶。求该青蛙跳上一个n级的台阶总共有多少种跳法。
如果只有1级台阶,只有一种跳法。如果有2级台阶,有两种跳法。我们把n级台阶时的跳法看成n的函数,记为f(n)。当n>2时,第一次跳的时候有两种选择:一是第一次跳一级,此时跳法数目等于后面剩下的n-1级台阶的跳法数目,即f(n-1);二是第一次跳2级,此时跳法数目等于后面剩下的n-2级台阶的跳法数目,即f(n-2)。因此,n级台阶的不同跳法的总数f(n)=f(n-1)+f(n-2)。分析到这里,不难看出这实际上就是斐波那契数列了。
题目拓展:在青蛙跳台阶的问题中,如果把条件改为:一只青蛙一次可以跳上1级台阶,也可也跳上2级台阶…它也可以跳上n级,此时该青蛙跳上一个n级的台阶总共有多少种跳法?
我们用数学归纳法可以证明f(n)=2^(n-1)
相关题目:我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用8个2*1的小矩形无重叠地覆盖一个2*8的大矩形,总共有多少种方法?
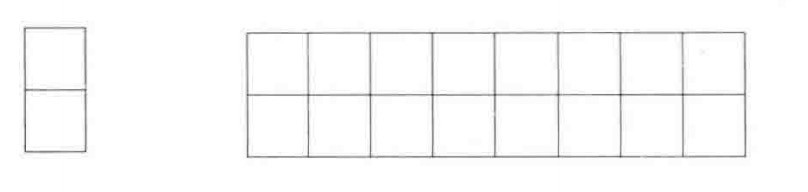
我们先把2*8的覆盖方法记为f(8)。用第一个2*1的小矩形去覆盖大矩形最左边时有两种选择:竖着放或者横着放。当竖着放时,右边还剩下2*7的区域,这种情形下的覆盖方法记为f(7)。接下来考虑横着放的情况。当2*1的小矩形横着放在左上角时,左下角必须横着放一个2*1的小矩形,此时右边还剩下2*6的区域,这种情形下的覆盖方法记为f(6)。因此f(8)=f(7)+f(6),仍然是斐波那契数列。
旋转数组的最小数字
题目:把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个递增排序的数组的一个旋转,输出旋转数组的最小元素。例如数组{3, 4, 5, 1, 2}为{1, 2, 3, 4, 5}的一个旋转,该数组的最小值为1。
传统思路:
从头到尾遍历数组一次,我们就能找出最小的元素,这种思路时间复杂度是O(n)。
新思路:
注意到选择之后的数组实际上可以划分为两个排序的子数组,而且前面的子数组的元素都大于或等于后面的子数组的元素。还注意到最小的元素刚好是这两个子数组的分界线,所以可以使用二分查找来实现O(logn)。
我们用两个指针分别指向数组的第一个元素和最后一个元素,按照题目中选择的规则,第一个元素应该是大于或者等于最后一个元素的(旋转数量为0时除外)。
接着我们可以找到数组中间的元素。如果该中间元素位于前面的递增子数组,那么它应该大于或者等于第一个指针指向的元素。此时数组中最小的元素应该位于该中间元素后面。我们可以把第一个指针指向该中间元素,这样可以缩小寻找的范围。移动之后的第一个指针仍然位于前面的递增子数组。
同样,如果中间元素位于后面的递增子数组,那么它应该小于或者等于第二个指针指向的元素。此时该数组中最小的元素应该位于该中间元素的前面。我们可以把第二个指针指向该中间元素吗,这样也可以缩小寻找的范围。移动之后的第二个指针仍然位于后面的递增子数组。
不管是移动第一个指针还是第二个指针,查找范围都会缩小到原来的一半。接下来我们再用更新之后的两个指针重复做新一轮的查找。以数组{3,4,5,1,2}为例:
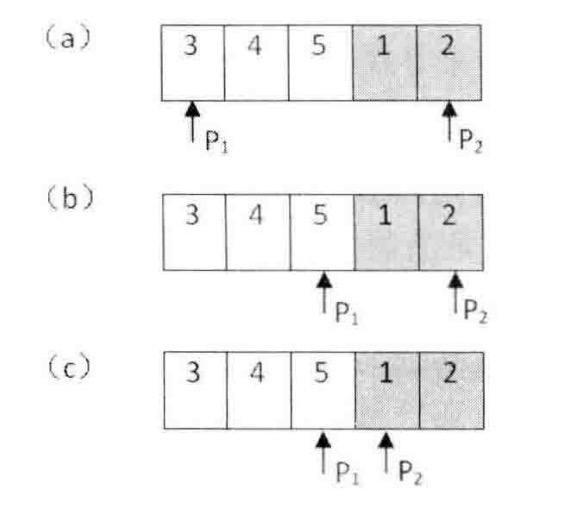
此外还需注意当数组中存在相同元素的时候,如数组{1,0,1,1,1}和数组{1,1,1,0,1}都可以看成递增排序数组{0,1,1,1,1}的旋转,如图分别画出它们由最小数字分隔开的两个子数组:

在这两个数组中,第一个数字、最后一个数字和中间数字都是1,我们无法确定中间的数字1是属于第一个递增子数组还是属于第二个递增子数组。因此,当两个指针指向的数字及它们中间的数字三者相同的时候,我们不得不采用顺序查找的方法。
#include <exception>
int MinInOrder(int* numbers, int index1, int index2);
int Min(int* numbers, int length)
{
if(numbers == nullptr || length <= 0)
throw new std::exception("Invalid parameters");
int index1 = 0;
int index2 = length - 1;
int indexMid = index1;
while(numbers[index1] >= numbers[index2])
{
// 如果index1和index2指向相邻的两个数,
// 则index1指向第一个递增子数组的最后一个数字,
// index2指向第二个子数组的第一个数字,也就是数组中的最小数字
if(index2 - index1 == 1)
{
indexMid = index2;
break;
}
// 如果下标为index1、index2和indexMid指向的三个数字相等,
// 则只能顺序查找
indexMid = (index1 + index2) / 2;
if(numbers[index1] == numbers[index2] && numbers[indexMid] == numbers[index1])
return MinInOrder(numbers, index1, index2);
// 缩小查找范围
if(numbers[indexMid] >= numbers[index1])
index1 = indexMid;
else if(numbers[indexMid] <= numbers[index2])
index2 = indexMid;
}
return numbers[indexMid];
}
int MinInOrder(int* numbers, int index1, int index2)
{
int result = numbers[index1];
for(int i = index1 + 1; i <= index2; ++i)
{
if(result > numbers[i])
result = numbers[i];
}
return result;
}
前面我们提到,在旋转数组中,有一个特例:如果把排序数组的前面0个元素搬到最后面,即排序数组本身,这仍然是数组的一个旋转。此时,数组中的第一个数字就是最小的数字,可以直接返回。这就是上面代码中,把indexMid初始化为index1的原因。
矩阵中的路径
题目:请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中任意一格开始,每一步可以在矩阵中向左、右、上、下移动一格。如果一条路径经过了矩阵的某一格,那么该路径不能再次进入该格子。例如在下面的3×4的矩阵中包含一条字符串“bfce”的路径(路径中的字母用下划线标出)。但矩阵中不包含字符串“abfb”的路径,因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后,路径不能再次进入这个格子。
A B T G C F C S J D E H
思路:
这是一个可以用回溯法解决的典型题,回溯法可以看成蛮力法的升级版。路径可以被看成一个栈。当在矩阵中定位了路径中前n个字符的位置之后,在与第n个字符对应的格子的周围都没有找到第n+1个字符,这时候只好在路径上回到第n-1个字符,重新定位第n个字符。
由于路径不能重复进入矩阵的格子,所以还需要定义和字符矩阵大小一样的布尔值矩阵,用来标志路径是否已经进入每个格子。
bool hasPathCore(const char* matrix, int rows, int cols, int row, int col, const char* str, int& pathLength, bool* visited);
bool hasPath(const char* matrix, int rows, int cols, const char* str)
{
if(matrix == nullptr || rows < 1 || cols < 1 || str == nullptr)
return false;
bool *visited = new bool[rows * cols];
memset(visited, 0, rows * cols);
int pathLength = 0;
for(int row = 0; row < rows; ++row)
{
for(int col = 0; col < cols; ++col)
{
if(hasPathCore(matrix, rows, cols, row, col, str,
pathLength, visited))
{
return true;
}
}
}
delete[] visited;
return false;
}
bool hasPathCore(const char* matrix, int rows, int cols, int row,
int col, const char* str, int& pathLength, bool* visited)
{
if(str[pathLength] == '\0')
return true;
bool hasPath = false;
if(row >= 0 && row < rows && col >= 0 && col < cols
&& matrix[row * cols + col] == str[pathLength]
&& !visited[row * cols + col])
{
++pathLength;
visited[row * cols + col] = true;
hasPath = hasPathCore(matrix, rows, cols, row, col - 1,
str, pathLength, visited)
|| hasPathCore(matrix, rows, cols, row - 1, col,
str, pathLength, visited)
|| hasPathCore(matrix, rows, cols, row, col + 1,
str, pathLength, visited)
|| hasPathCore(matrix, rows, cols, row + 1, col,
str, pathLength, visited);
if(!hasPath)
{
--pathLength;
visited[row * cols + col] = false;
}
}
return hasPath;
}
机器人的运动范围
题目:地上有一个m行n列的方格。一个机器人从坐标(0, 0)的格子开始移动,它每一次可以向左、右、上、下移动一格,但不能进入行坐标和列坐标的数位之和大于k的格子。例如,当k为18时,机器人能够进入方格(35, 37),因为3+5+3+7=18。但它不能进入方格(35, 38),因为3+5+3+8=19。请问该机器人能够到达多少个格子?
思路:
和前面的题目类似,这个方格也可以看作一个m*n的矩阵。机器人从坐标(0,0)开始移动,当它准备进入坐标(i,j)的格子时,通过检查坐标的位数来判断机器人是否能够进入。如果机器人能够进入,则再判断它能否进入4个相邻的格子。
int movingCountCore(int threshold, int rows, int cols, int row, int col, bool* visited);
bool check(int threshold, int rows, int cols, int row, int col, bool* visited);
int getDigitSum(int number);
int movingCount(int threshold, int rows, int cols)
{
if(threshold < 0 || rows <= 0 || cols <= 0)
return 0;
bool *visited = new bool[rows * cols];
for(int i = 0; i < rows * cols; ++i)
visited[i] = false;
int count = movingCountCore(threshold, rows, cols,
0, 0, visited);
delete[] visited;
return count;
}
int movingCountCore(int threshold, int rows, int cols, int row,
int col, bool* visited)
{
int count = 0;
if(check(threshold, rows, cols, row, col, visited))
{
visited[row * cols + col] = true;
count = 1 + movingCountCore(threshold, rows, cols,
row - 1, col, visited)
+ movingCountCore(threshold, rows, cols,
row, col - 1, visited)
+ movingCountCore(threshold, rows, cols,
row + 1, col, visited)
+ movingCountCore(threshold, rows, cols,
row, col + 1, visited);
}
return count;
}
bool check(int threshold, int rows, int cols, int row, int col,
bool* visited)
{
if(row >= 0 && row < rows && col >= 0 && col < cols
&& getDigitSum(row) + getDigitSum(col) <= threshold
&& !visited[row* cols + col])
return true;
return false;
}
int getDigitSum(int number)
{
int sum = 0;
while(number > 0)
{
sum += number % 10;
number /= 10;
}
return sum;
}
剪绳子
题目:给你一根长度为n绳子,请把绳子剪成m段(m、n都是整数,n>1并且m≥1)。每段的绳子的长度记为k[0]、k[1]、……、k[m]。k[0]*k[1]…*k[m]可能的最大乘积是多少?例如当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到最大的乘积18。
动态规划:
定义函数f(n)为把长度为n的绳子剪成若干段后个段长度乘积的最大值。再减第一刀的时候,我们有n-1种可能的选择,也就是剪出来的第一段绳子的可能长度分别为1,2,…,n-1。因此f(n)=max(f(i)*f(n-i)),其中0<i<n。
这是一个从上至下的递归公式。由于递归会有很多重复的子问题,从而有大量不必要的重复计算。一个更好的办法是按照从下而上的顺序计算,也就是我们先得到f(2)、f(3),再得到f(4)、f(5),直到得到f(n)。
int maxProductAfterCutting_solution1(int length)
{
if(length < 2)
return 0;
if(length == 2)
return 1;
if(length == 3)
return 2;
int* products = new int[length + 1];
products[0] = 0;
products[1] = 1;
products[2] = 2;
products[3] = 3;
int max = 0;
for(int i = 4; i <= length; ++i)
{
max = 0;
for(int j = 1; j <= i / 2; ++j)
{
int product = products[j] * products[i - j];
if(max < product)
max = product;
}
products[i] = max;
}
max = products[length];
delete[] products;
return max;
}
贪婪算法:
如果我们按照如下策略来剪绳子,则得到的各段绳子的长度的乘积将最大:当n>=5时,我们尽可能多的剪长度为3的绳子;当剩下的绳子长度为4时,把绳子剪成两段长度为2的绳子。
证明:当n>=5时,我们可以证明2(n-2)>n并且3(n-3)>n。也就是说,当绳子剩下的长度大于或者等于5的时候,我们就把它剪成长度为3或者2的绳子段。另外,当n>=5时,3(n-3)>=2(n-2),因此我们应该尽可能地多剪长度为3的绳子。
int maxProductAfterCutting_solution2(int length)
{
if(length < 2)
return 0;
if(length == 2)
return 1;
if(length == 3)
return 2;
// 尽可能多地减去长度为3的绳子段
int timesOf3 = length / 3;
// 当绳子最后剩下的长度为4的时候,不能再剪去长度为3的绳子段。
// 此时更好的方法是把绳子剪成长度为2的两段,因为2*2 > 3*1。
if(length - timesOf3 * 3 == 1)
timesOf3 -= 1;
int timesOf2 = (length - timesOf3 * 3) / 2;
return (int) (pow(3, timesOf3)) * (int) (pow(2, timesOf2));
}
二进制中1的个数
题目:请实现一个函数,输入一个整数,输出该数二进制表示中1的个数。例如把9表示成二进制是1001,有2位是1。因此如果输入9,该函数输出2。
int NumberOf1_Solution1(int n)
{
int count = 0;
unsigned int flag = 1;
while (flag)
{
if (n & flag)
count++;
flag = flag << 1;
}
return count;
}
这个解法中,循环的次数等于整数二进制的位数,32位的整数需要循环32次。下面再介绍一种算法,整数中有几个1就只需要循环几次。
int NumberOf1_Solution2(int n)
{
int count = 0;
while (n)
{
++count;
n = (n - 1) & n;
}
return count;
}
把一个整数减去1,再和原整数做与运算,会把该整数最右边的1变成0。那么一个整数的二进制表示中有多少个1,就可以进行多少次这样的操作。
相关题目:
-
用一条语句判断一个整数是不是2的整数次方。一个整数如果是2的整数次方,那么它的二进制表示中有且只有一位是1,而其他所有位都是0。根据前面的分析,把这个整数减去1之后再和它自己做与运算,这个整数中唯一的1就会变成0。
-
输入两个整数m和n,计算需要改变m的二进制表示中的多少位才能得到n。比如10的二进制表示为1010,12的二进制表示为1101,需要改变1010中的3位才能得到1101。我们可以分两步解决这个问题:第一步求这两个数的异或;第二步统计异或结果中1的位数。
数值的整数次方
题目:实现函数double Power(double base, int exponent),求base的exponent次方。不得使用库函数,同时不需要考虑大数问题。
bool g_InvalidInput = false;
bool equal(double num1, double num2);
double PowerWithUnsignedExponent(double base, unsigned int exponent);
double Power(double base, int exponent)
{
g_InvalidInput = false;
if (equal(base, 0.0) && exponent < 0)
{
g_InvalidInput = true;
return 0.0;
}
unsigned int absExponent = (unsigned int) (exponent);
if (exponent < 0)
absExponent = (unsigned int) (-exponent);
double result = PowerWithUnsignedExponent(base, absExponent);
if (exponent < 0)
result = 1.0 / result;
return result;
}
double PowerWithUnsignedExponent(double base, unsigned int exponent)
{
if (exponent == 0)
return 1;
if (exponent == 1)
return base;
double result = PowerWithUnsignedExponent(base, exponent >> 1);
result *= result;
if ((exponent & 0x1) == 1)
result *= base;
return result;
}
bool equal(double num1, double num2)
{
if ((num1 - num2 > -0.0000001) && (num1 - num2 < 0.0000001))
return true;
else
return false;
}
如果输入指数位32,采用累计相乘需要做31次乘法。我们可以换一种思路:我们的目标是求一个数字的32次方,如果我们知道了它的16次方,那么只要在16次方的基础上再平方一次就可以了。而16次方是8次方的平方。这样以此类推,我们求32次方只需要做5次乘法。我们可以使用递归来实现这个步骤。
使用右移运算符代替除以2,用位与运算符代替了求余运算符(%)来判断一个数是奇数还是偶数。位运算的效率比乘除法及求余运算的效率要高很多。
打印1到最大的n位数
题目:输入数字n,按顺序打印出从1最大的n位十进制数。比如输入3,则 打印出1、2、3一直到最大的3位数即999。
当n很大时,我们求最大的n位数用整型(int)或长整型(long long)都会溢出。也就是说我们需要考虑大数问题。最常用的方法是用字符串或数组来表达大数,我们需要做两件事情:一是在字符串表达的数字上模拟加法;二是把字符串表达的数字打印出来。
void PrintNumber(char* number);
bool Increment(char* number);
void Print1ToMaxOfNDigitsRecursively(char* number, int length, int index);
// ====================方法一====================
void Print1ToMaxOfNDigits_1(int n)
{
if (n <= 0)
return;
char *number = new char[n + 1];
memset(number, '0', n);
number[n] = '\0';
while (!Increment(number))
{
PrintNumber(number);
}
delete[]number;
}
// 字符串number表示一个数字,在 number上增加1
// 如果做加法溢出,则返回true;否则为false
bool Increment(char* number)
{
bool isOverflow = false;
int nTakeOver = 0;
int nLength = strlen(number);
for (int i = nLength - 1; i >= 0; i--)
{
int nSum = number[i] - '0' + nTakeOver;
if (i == nLength - 1)
nSum++;
if (nSum >= 10)
{
if (i == 0)
isOverflow = true;
else
{
nSum -= 10;
nTakeOver = 1;
number[i] = '0' + nSum;
}
}
else
{
number[i] = '0' + nSum;
break;
}
}
return isOverflow;
}
// ====================方法二====================
void Print1ToMaxOfNDigits_2(int n)
{
if (n <= 0)
return;
char* number = new char[n + 1];
number[n] = '\0';
for (int i = 0; i < 10; ++i)
{
number[0] = i + '0';
Print1ToMaxOfNDigitsRecursively(number, n, 0);
}
delete[] number;
}
void Print1ToMaxOfNDigitsRecursively(char* number, int length, int index)
{
if (index == length - 1)
{
PrintNumber(number);
return;
}
for (int i = 0; i < 10; ++i)
{
number[index + 1] = i + '0';
Print1ToMaxOfNDigitsRecursively(number, length, index + 1);
}
}
// ====================公共函数====================
// 字符串number表示一个数字,数字有若干个0开头
// 打印出这个数字,并忽略开头的0
void PrintNumber(char* number)
{
bool isBeginning0 = true;
int nLength = strlen(number);
for (int i = 0; i < nLength; ++i)
{
if (isBeginning0 && number[i] != '0')
isBeginning0 = false;
if (!isBeginning0)
{
printf("%c", number[i]);
}
}
printf("\t");
}
接下来我们换一种思路,如果我们在数字前面补0,就会发现n位所有十进制数其实就是n个从0到9的全排列。也就是说,我们把数字的每一位都从0到9排列一遍,就得到来所有的十进制数。
全排列用递归很容易表达,数字的每一位都可能是0~9中的一个数,然后设置下一位。递归结束的条件是我们已经设置来数字的最后一位。
相关题目:定义一个函数,在该函数中可以实现任意两个数字的加法。由于没有限定输入两个数的大小范围,我们也要把它当作大数问题来处理。在前面的代码的第一种思路中,实现来在字符串表示的数字上加1的功能,我们可以参考这种思路实现两个数字的相加功能。另外还有一个需要注意的问题:如果输入的数字中由负数,那么我们应该怎么处理?
删除链表的节点
题目:给定单向链表的头指针和一个结点指针,定义一个函数在O(1)时间删除该结点。
不一定需要得到被删除的节点的前一个节点,我们可以把下一个节点的内容复制到需要删除的节点上覆盖原有的内容,再把下一个节点删除。
void DeleteNode(ListNode** pListHead, ListNode* pToBeDeleted)
{
if(!pListHead || !pToBeDeleted)
return;
// 要删除的结点不是尾结点
if(pToBeDeleted->m_pNext != nullptr)
{
ListNode* pNext = pToBeDeleted->m_pNext;
pToBeDeleted->m_nValue = pNext->m_nValue;
pToBeDeleted->m_pNext = pNext->m_pNext;
delete pNext;
pNext = nullptr;
}
// 链表只有一个结点,删除头结点(也是尾结点)
else if(*pListHead == pToBeDeleted)
{
delete pToBeDeleted;
pToBeDeleted = nullptr;
*pListHead = nullptr;
}
// 链表中有多个结点,删除尾结点
else
{
ListNode* pNode = *pListHead;
while(pNode->m_pNext != pToBeDeleted)
{
pNode = pNode->m_pNext;
}
pNode->m_pNext = nullptr;
delete pToBeDeleted;
pToBeDeleted = nullptr;
}
}
题目:在一个排序的链表中,如何删除重复的结点?
我们从头遍历整个链表,如果当前节点的值与下一个节点的值相同,那么它们就是重重的节点,都可以被删除。为了保证删除之后的链表仍然是相连的,我们要把当前节点的前一个节点和后面值比当前节点的值大的节点相连。我们要确保pPreNode始终与下一个没有重复的节点连接在一起。
void DeleteDuplication(ListNode** pHead)
{
if(pHead == nullptr || *pHead == nullptr)
return;
ListNode* pPreNode = nullptr;
ListNode* pNode = *pHead;
while(pNode != nullptr)
{
ListNode *pNext = pNode->m_pNext;
bool needDelete = false;
if(pNext != nullptr && pNext->m_nValue == pNode->m_nValue)
needDelete = true;
if(!needDelete)
{
pPreNode = pNode;
pNode = pNode->m_pNext;
}
else
{
int value = pNode->m_nValue;
ListNode* pToBeDel = pNode;
while(pToBeDel != nullptr && pToBeDel->m_nValue == value)
{
pNext = pToBeDel->m_pNext;
delete pToBeDel;
pToBeDel = nullptr;
pToBeDel = pNext;
}
if(pPreNode == nullptr)
*pHead = pNext;
else
pPreNode->m_pNext = pNext;
pNode = pNext;
}
}
}
正则表达式匹配
题目:请实现一个函数用来匹配包含'.'和'*'的正则表达式。模式中的字符'.'表示任意一个字符,而'*'表示它前面的字符可以出现任意次(含0次)。在本题中,匹配是指字符串的所有字符匹配整个模式。例如,字符串"aaa"与模式"a.a"和"ab*ac*a"匹配,但与"aa.a"及"ab*a"均不匹配。
bool matchCore(const char* str, const char* pattern);
bool match(const char* str, const char* pattern)
{
if(str == nullptr || pattern == nullptr)
return false;
return matchCore(str, pattern);
}
bool matchCore(const char* str, const char* pattern)
{
if(*str == '\0' && *pattern == '\0')
return true;
if(*str != '\0' && *pattern == '\0')
return false;
if(*(pattern + 1) == '*')
{
if(*pattern == *str || (*pattern == '.' && *str != '\0'))
// 进入有限状态机的下一个状态
return matchCore(str + 1, pattern + 2)
// 继续留在有限状态机的当前状态
|| matchCore(str + 1, pattern)
// 略过一个'*'
|| matchCore(str, pattern + 2);
else
// 略过一个'*'
return matchCore(str, pattern + 2);
}
if(*str == *pattern || (*pattern == '.' && *str != '\0'))
return matchCore(str + 1, pattern + 1);
return false;
}
表示数值的字符串
题目:请实现一个函数用来判断字符串是否表示数值(包括整数和小数)。例如,字符串“+100”、“5e2”、“-123”、“3.1416”及“-1E-16”都表示数值,但“12e”、“1a3.14”、“1.2.3”、“+-5”及“12e+5.4”都不是
bool scanUnsignedInteger(const char** str);
bool scanInteger(const char** str);
// 数字的格式可以用A[.[B]][e|EC]或者.B[e|EC]表示,其中A和C都是
// 整数(可以有正负号,也可以没有),而B是一个无符号整数
bool isNumeric(const char* str)
{
if(str == nullptr)
return false;
bool numeric = scanInteger(&str);
// 如果出现'.',接下来是数字的小数部分
if(*str == '.')
{
++str;
// 下面一行代码用||的原因:
// 1. 小数可以没有整数部分,例如.123等于0.123;
// 2. 小数点后面可以没有数字,例如233.等于233.0;
// 3. 当然小数点前面和后面可以有数字,例如233.666
numeric = scanUnsignedInteger(&str) || numeric;
}
// 如果出现'e'或者'E',接下来跟着的是数字的指数部分
if(*str == 'e' || *str == 'E')
{
++str;
// 下面一行代码用&&的原因:
// 1. 当e或E前面没有数字时,整个字符串不能表示数字,例如.e1、e1;
// 2. 当e或E后面没有整数时,整个字符串不能表示数字,例如12e、12e+5.4
numeric = numeric && scanInteger(&str);
}
return numeric && *str == '\0';
}
bool scanUnsignedInteger(const char** str)
{
const char* before = *str;
while(**str != '\0' && **str >= '0' && **str <= '9')
++(*str);
// 当str中存在若干0-9的数字时,返回true
return *str > before;
}
// 整数的格式可以用[+|-]B表示, 其中B为无符号整数
bool scanInteger(const char** str)
{
if(**str == '+' || **str == '-')
++(*str);
return scanUnsignedInteger(str);
}
调整数组顺序使奇数位于偶数前面
题目:输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有奇数位于数组的前半部分,所有偶数位于数组的后半部分。
void Reorder(int *pData, unsigned int length, bool (*func)(int));
bool isEven(int n);
// ====================方法一====================
void ReorderOddEven_1(int *pData, unsigned int length)
{
if(pData == nullptr || length == 0)
return;
int *pBegin = pData;
int *pEnd = pData + length - 1;
while(pBegin < pEnd)
{
// 向后移动pBegin,直到它指向偶数
while(pBegin < pEnd && (*pBegin & 0x1) != 0)
pBegin ++;
// 向前移动pEnd,直到它指向奇数
while(pBegin < pEnd && (*pEnd & 0x1) == 0)
pEnd --;
if(pBegin < pEnd)
{
int temp = *pBegin;
*pBegin = *pEnd;
*pEnd = temp;
}
}
}
// ====================方法二====================
void ReorderOddEven_2(int *pData, unsigned int length)
{
Reorder(pData, length, isEven);
}
void Reorder(int *pData, unsigned int length, bool (*func)(int))
{
if(pData == nullptr || length == 0)
return;
int *pBegin = pData;
int *pEnd = pData + length - 1;
while(pBegin < pEnd)
{
// 向后移动pBegin
while(pBegin < pEnd && !func(*pBegin))
pBegin ++;
// 向前移动pEnd
while(pBegin < pEnd && func(*pEnd))
pEnd --;
if(pBegin < pEnd)
{
int temp = *pBegin;
*pBegin = *pEnd;
*pEnd = temp;
}
}
}
bool isEven(int n)
{
return (n & 1) == 0;
}
如果把问题改成将数组中的负数移到非负数的前面,或者把能被3整除的数移到不能被3整除的数的前面,都只需定义新的函数来确定分组的标准。解耦的好处就是提高来代码的重用性,为功能拓展提供了便利。
链表中倒数第k个结点
题目:输入一个链表,输出该链表中倒数第k个结点。为了符合大多数人的习惯,本题从1开始计数,即链表的尾结点是倒数第1个结点。例如一个链表有6个结点,从头结点开始它们的值依次是1、2、3、4、5、6。这个链表的倒数第3个结点是值为4的结点。
ListNode* FindKthToTail(ListNode* pListHead, unsigned int k)
{
if(pListHead == nullptr || k == 0)
return nullptr;
ListNode *pAhead = pListHead;
ListNode *pBehind = nullptr;
for(unsigned int i = 0; i < k - 1; ++ i)
{
if(pAhead->m_pNext != nullptr)
pAhead = pAhead->m_pNext;
else
{
return nullptr;
}
}
pBehind = pListHead;
while(pAhead->m_pNext != nullptr)
{
pAhead = pAhead->m_pNext;
pBehind = pBehind->m_pNext;
}
return pBehind;
}
相关题目:求链表的中间节点。如果链表中的节点总数为奇数,则返回中间节点;如果节点总数是偶数,则返回中间两个节点的任意一个。为了解决这个问题,我们也可以定义两个指针,同时从链表的头节点出发,一个指针一次走一步,另一个指针一次走两步。当走得快的指针走到链表的末尾时,走得慢的指针正好在链表的中间。
链表中环的入口结点
题目:一个链表中包含环,如何找出环的入口结点?例如,下图链表中,环的入口结点是结点3。
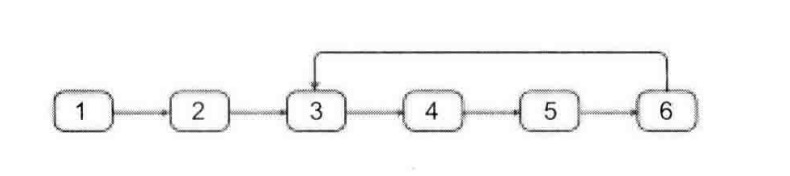
解决这个问题的第一步是如果确定一个链表中包含环。定义两个指针同时从链表的头节点出发,一个指针一次走一步,另一个指针一次走两步。如果走得快的指针追上了走得慢的指针,那么链表就包含环;如果走得快的指针走到了链表的末尾都没有追上,那么链表就不包含环。
第二步是如何找到环的入口。先定义两个指针P1和P2指向链表的头节点。如果链表中的环有n个节点,则指针P1先在链表上向前移动n步,然后两个指针以相同的速度向前移动。当第二个指针指向环的入口节点时,第一个指针已经围绕着环走了一圈,又回到了入口节点。
剩下的问题是如何得到环中节点的数目。我们可以从相遇的节点出发,一边继续向前移动一边计数,当再次回到这个节点时,就可以得到环中节点数了。
ListNode* MeetingNode(ListNode* pHead)
{
if(pHead == nullptr)
return nullptr;
ListNode* pSlow = pHead->m_pNext;
if(pSlow == nullptr)
return nullptr;
ListNode* pFast = pSlow->m_pNext;
while(pFast != nullptr && pSlow != nullptr)
{
if(pFast == pSlow)
return pFast;
pSlow = pSlow->m_pNext;
pFast = pFast->m_pNext;
if(pFast != nullptr)
pFast = pFast->m_pNext;
}
return nullptr;
}
ListNode* EntryNodeOfLoop(ListNode* pHead)
{
ListNode* meetingNode = MeetingNode(pHead);
if(meetingNode == nullptr)
return nullptr;
// 得到环中结点的数目
int nodesInLoop = 1;
ListNode* pNode1 = meetingNode;
while(pNode1->m_pNext != meetingNode)
{
pNode1 = pNode1->m_pNext;
++nodesInLoop;
}
// 先移动pNode1,次数为环中结点的数目
pNode1 = pHead;
for(int i = 0; i < nodesInLoop; ++i)
pNode1 = pNode1->m_pNext;
// 再移动pNode1和pNode2
ListNode* pNode2 = pHead;
while(pNode1 != pNode2)
{
pNode1 = pNode1->m_pNext;
pNode2 = pNode2->m_pNext;
}
return pNode1;
}
反转链表
题目:定义一个函数,输入一个链表的头结点,反转该链表并输出反转后链表的头结点。
这里需要定义3个指针,分别指向当前遍历到的节点、它的前一个节点及后一个节点。
ListNode* ReverseList(ListNode* pHead)
{
ListNode* pReversedHead = nullptr;
ListNode* pNode = pHead;
ListNode* pPrev = nullptr;
while(pNode != nullptr)
{
ListNode* pNext = pNode->m_pNext;
if(pNext == nullptr)
pReversedHead = pNode;
pNode->m_pNext = pPrev;
pPrev = pNode;
pNode = pNext;
}
return pReversedHead;
}
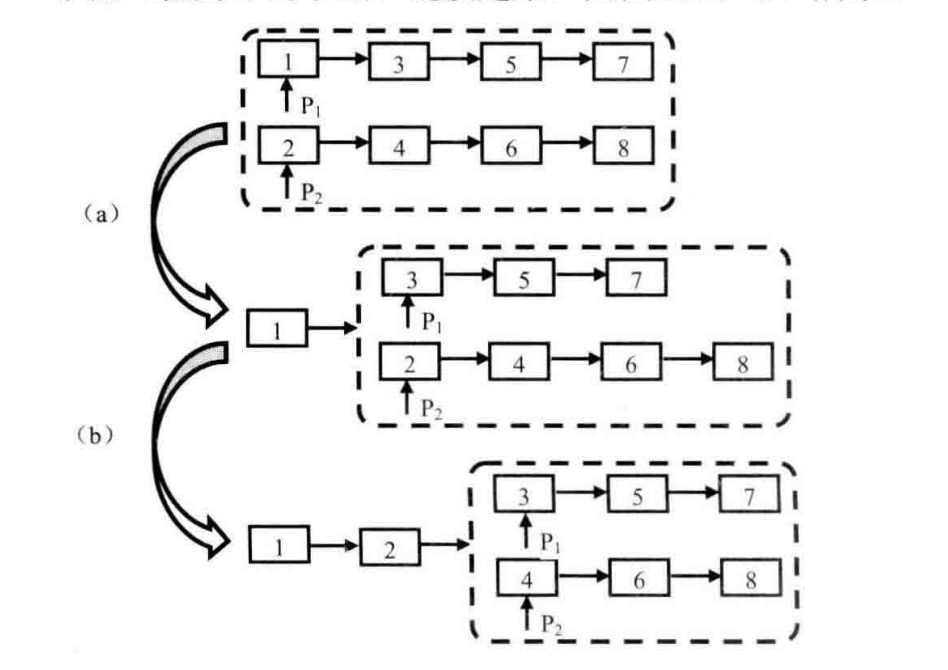
合并两个排序的链表
题目:输入两个递增排序的链表,合并这两个链表并使新链表中的结点仍然是按照递增排序的。
ListNode* Merge(ListNode* pHead1, ListNode* pHead2)
{
if(pHead1 == nullptr)
return pHead2;
else if(pHead2 == nullptr)
return pHead1;
ListNode* pMergedHead = nullptr;
if(pHead1->m_nValue < pHead2->m_nValue)
{
pMergedHead = pHead1;
pMergedHead->m_pNext = Merge(pHead1->m_pNext, pHead2);
}
else
{
pMergedHead = pHead2;
pMergedHead->m_pNext = Merge(pHead1, pHead2->m_pNext);
}
return pMergedHead;
}
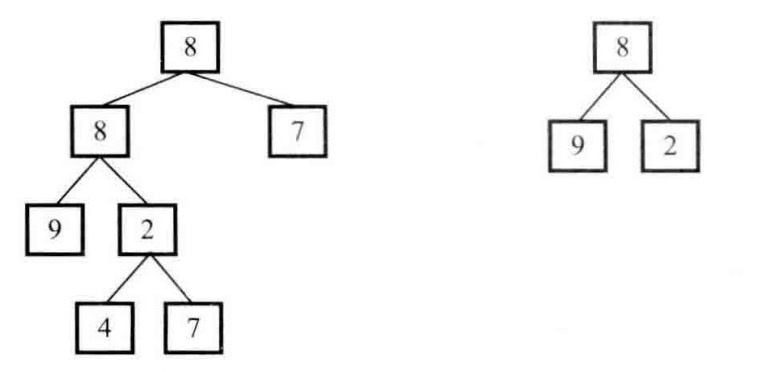
树的子结构
题目:输入两棵二叉树A和B,判断B是不是A的子结构。
思路:
第一步在树中查找与根结点一样的节点,这实际上就是树的遍历。对二叉树这种数据结构熟悉的自然知道可以用递归的方法去遍历。
第二步是判断树A中以R为根结点的子树是不是和树B具有相同的结构。同样,我们也可以用递归的思路来考虑。
struct BinaryTreeNode
{
double m_dbValue;
BinaryTreeNode* m_pLeft;
BinaryTreeNode* m_pRight;
};
bool DoesTree1HaveTree2(BinaryTreeNode* pRoot1, BinaryTreeNode* pRoot2);
bool Equal(double num1, double num2);
bool HasSubtree(BinaryTreeNode* pRoot1, BinaryTreeNode* pRoot2)
{
bool result = false;
if(pRoot1 != nullptr && pRoot2 != nullptr)
{
if(Equal(pRoot1->m_dbValue, pRoot2->m_dbValue))
result = DoesTree1HaveTree2(pRoot1, pRoot2);
if(!result)
result = HasSubtree(pRoot1->m_pLeft, pRoot2);
if(!result)
result = HasSubtree(pRoot1->m_pRight, pRoot2);
}
return result;
}
bool DoesTree1HaveTree2(BinaryTreeNode* pRoot1, BinaryTreeNode* pRoot2)
{
if(pRoot2 == nullptr)
return true;
if(pRoot1 == nullptr)
return false;
if(!Equal(pRoot1->m_dbValue, pRoot2->m_dbValue))
return false;
return DoesTree1HaveTree2(pRoot1->m_pLeft, pRoot2->m_pLeft) &&
DoesTree1HaveTree2(pRoot1->m_pRight, pRoot2->m_pRight);
}
bool Equal(double num1, double num2)
{
if((num1 - num2 > -0.0000001) && (num1 - num2 < 0.0000001))
return true;
else
return false;
}
这里有个细节:本题节点中值的类型为double,由于计算机在表示小数(float和double)时存在误差,判断两个小数是否相等,只能判断它们之差的绝对值是不是在一个很小的范围内。
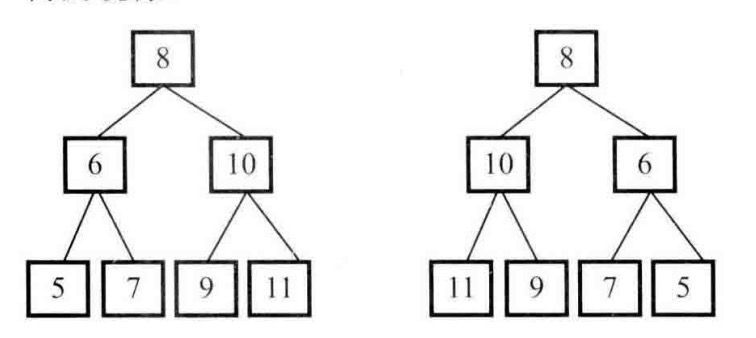
二叉树的镜像
题目:请完成一个函数,输入一个二叉树,该函数输出它的镜像。
// 递归
void MirrorRecursively(BinaryTreeNode *pNode)
{
if((pNode == nullptr) || (pNode->m_pLeft == nullptr && pNode->m_pRight))
return;
BinaryTreeNode *pTemp = pNode->m_pLeft;
pNode->m_pLeft = pNode->m_pRight;
pNode->m_pRight = pTemp;
if(pNode->m_pLeft)
MirrorRecursively(pNode->m_pLeft);
if(pNode->m_pRight)
MirrorRecursively(pNode->m_pRight);
}
// 循环
void MirrorIteratively(BinaryTreeNode* pRoot)
{
if(pRoot == nullptr)
return;
std::stack<BinaryTreeNode*> stackTreeNode;
stackTreeNode.push(pRoot);
while(stackTreeNode.size() > 0)
{
BinaryTreeNode *pNode = stackTreeNode.top();
stackTreeNode.pop();
BinaryTreeNode *pTemp = pNode->m_pLeft;
pNode->m_pLeft = pNode->m_pRight;
pNode->m_pRight = pTemp;
if(pNode->m_pLeft)
stackTreeNode.push(pNode->m_pLeft);
if(pNode->m_pRight)
stackTreeNode.push(pNode->m_pRight);
}
}
对称的二叉树
题目:请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。
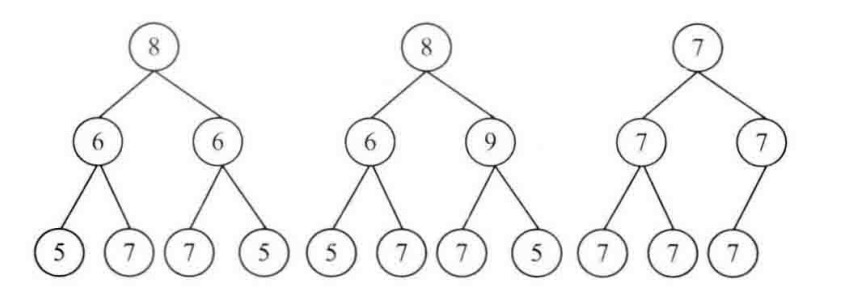
我们针对前序遍历定义一种对称的算法,即先遍历父节点,再遍历它的右子节点,最后遍历它的左子节点。我们发现可以通过比较二叉树的前序遍历序列和对称前序遍历序列来判断二叉树是不是对称的。如果两个序列一样,那么就是对称的。
bool isSymmetrical(BinaryTreeNode* pRoot1, BinaryTreeNode* pRoot2);
bool isSymmetrical(BinaryTreeNode* pRoot)
{
return isSymmetrical(pRoot, pRoot);
}
bool isSymmetrical(BinaryTreeNode* pRoot1, BinaryTreeNode* pRoot2)
{
if(pRoot1 == nullptr && pRoot2 == nullptr)
return true;
if(pRoot1 == nullptr || pRoot2 == nullptr)
return false;
if(pRoot1->m_nValue != pRoot2->m_nValue)
return false;
return isSymmetrical(pRoot1->m_pLeft, pRoot2->m_pRight)
&& isSymmetrical(pRoot1->m_pRight, pRoot2->m_pLeft);
}
顺时针打印矩阵
题目:输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字。例如,如果输入如下矩阵:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
则依次打印出数字1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10。
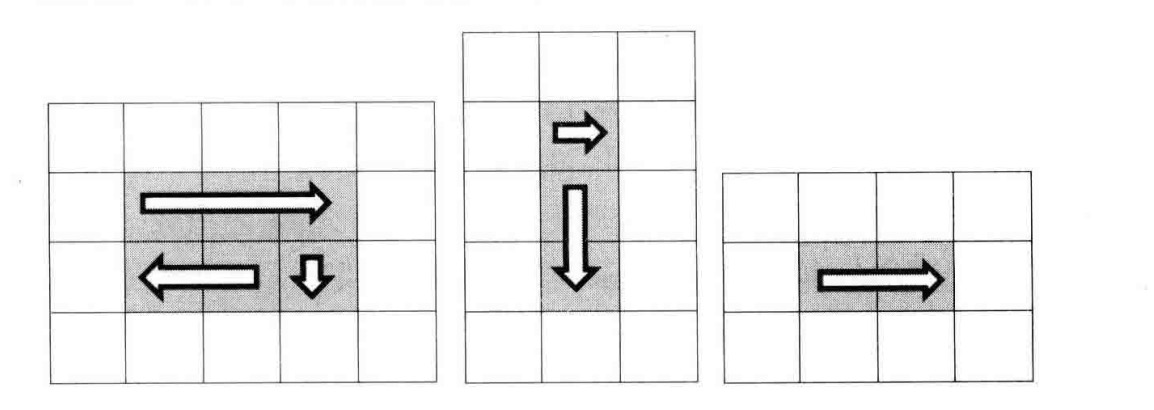
我们可以把矩阵想象成若干个圈,用一个循环来打印矩阵,每次打印矩阵中的一个圈。
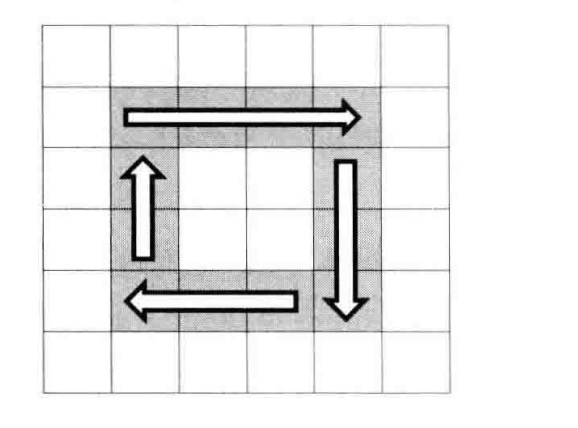
不过值得注意,最后一圈有可能退化成只要一行、只有一列,甚至只有一个数字,打印这样的一圈就不再需要四步。
void PrintMatrixInCircle(int** numbers, int columns, int rows, int start);
void printNumber(int number);
void PrintMatrixClockwisely(int** numbers, int columns, int rows)
{
if(numbers == nullptr || columns <= 0 || rows <= 0)
return;
int start = 0;
while(columns > start * 2 && rows > start * 2)
{
PrintMatrixInCircle(numbers, columns, rows, start);
++start;
}
}
void PrintMatrixInCircle(int** numbers, int columns, int rows, int start)
{
int endX = columns - 1 - start;
int endY = rows - 1 - start;
// 从左到右打印一行
for(int i = start; i <= endX; ++i)
{
int number = numbers[start][i];
printNumber(number);
}
// 从上到下打印一列
if(start < endY)
{
for(int i = start + 1; i <= endY; ++i)
{
int number = numbers[i][endX];
printNumber(number);
}
}
// 从右到左打印一行
if(start < endX && start < endY)
{
for(int i = endX - 1; i >= start; --i)
{
int number = numbers[endY][i];
printNumber(number);
}
}
// 从下到上打印一行
if(start < endX && start < endY - 1)
{
for(int i = endY - 1; i >= start + 1; --i)
{
int number = numbers[i][start];
printNumber(number);
}
}
}
void printNumber(int number)
{
printf("%d\t", number);
}
包含min函数的栈
题目:定义栈的数据结构,请在该类型中实现一个能够得到栈的最小元素的min函数。在该栈中,调用min、push及pop的时间复杂度都是O(1)。
思路:我们可以把每次的最小元素(之前的最小元素和新压入栈的元素两者的较小值)都保存起来放到另外一个辅助栈里。当最小元素从数据栈内被弹出之后,同时弹出辅助栈的栈顶元素,此时辅助栈的新栈顶元素就是下一个最小值。
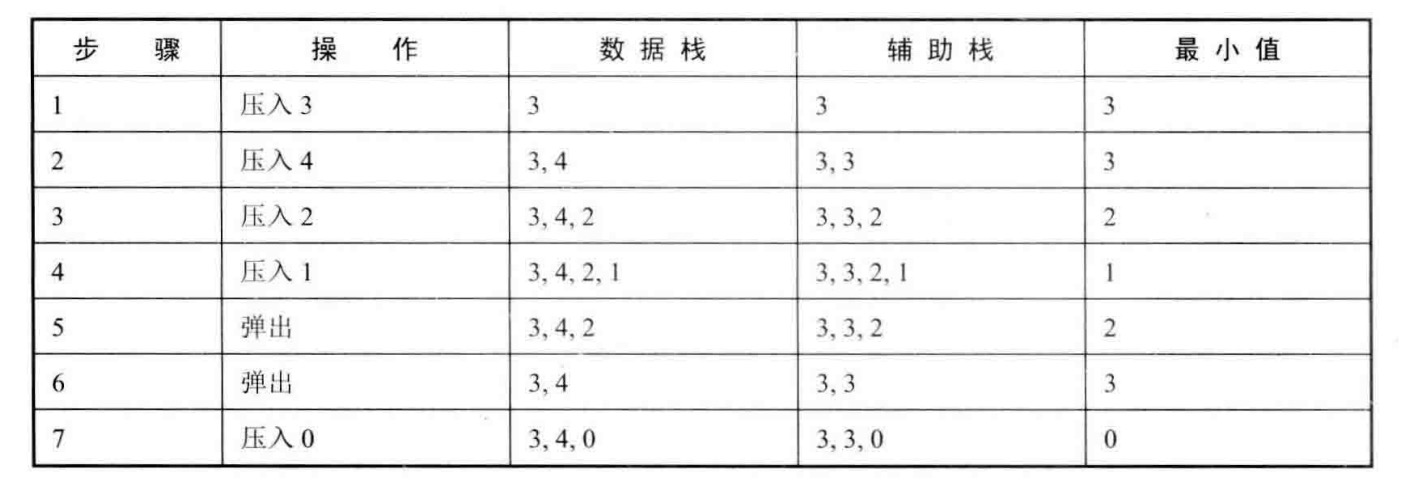
#include <stack>
#include <assert.h>
template <typename T> class StackWithMin
{
public:
StackWithMin() {}
virtual ~StackWithMin() {}
T& top();
const T& top() const;
void push(const T& value);
void pop();
const T& min() const;
bool empty() const;
size_t size() const;
private:
std::stack<T> m_data; // 数据栈,存放栈的所有元素
std::stack<T> m_min; // 辅助栈,存放栈的最小元素
};
template <typename T> void StackWithMin<T>::push(const T& value)
{
// 把新元素添加到辅助栈
m_data.push(value);
// 当新元素比之前的最小元素小时,把新元素插入辅助栈里;
// 否则把之前的最小元素重复插入辅助栈里
if(m_min.size() == 0 || value < m_min.top())
m_min.push(value);
else
m_min.push(m_min.top());
}
template <typename T> void StackWithMin<T>::pop()
{
assert(m_data.size() > 0 && m_min.size() > 0);
m_data.pop();
m_min.pop();
}
template <typename T> const T& StackWithMin<T>::min() const
{
assert(m_data.size() > 0 && m_min.size() > 0);
return m_min.top();
}
template <typename T> T& StackWithMin<T>::top()
{
return m_data.top();
}
template <typename T> const T& StackWithMin<T>::top() const
{
return m_data.top();
}
template <typename T> bool StackWithMin<T>::empty() const
{
return m_data.empty();
}
template <typename T> size_t StackWithMin<T>::size() const
{
return m_data.size();
}
栈的压入、弹出序列
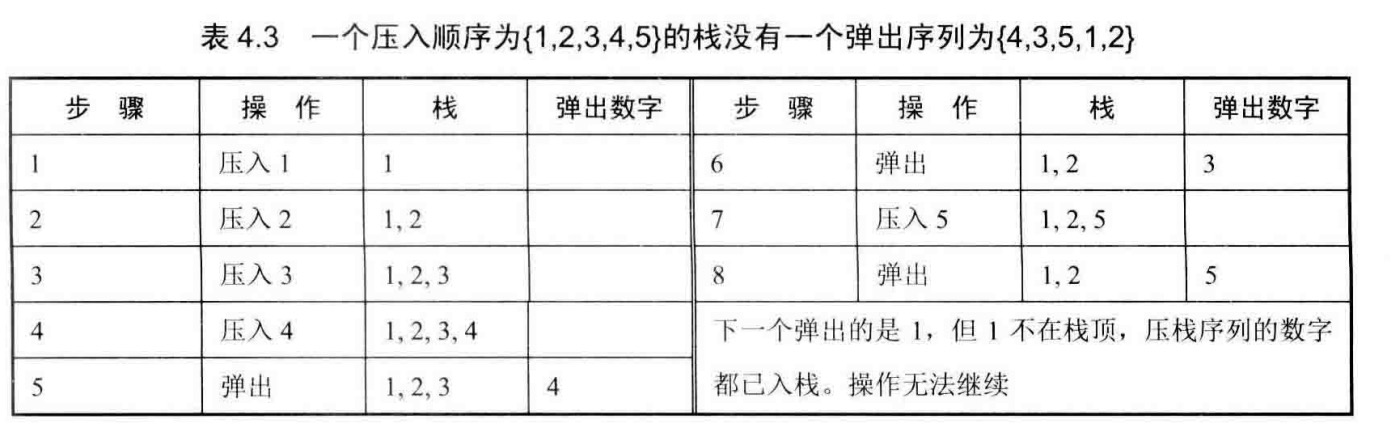
题目:输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1、2、3、4、5是某栈的压栈序列,序列4、5、3、2、1是该压栈序列对应的一个弹出序列,但4、3、5、1、2就不可能是该压栈序列的弹出序列。
思路:解决这个问题很直观的想法就是建立一个辅助栈。如果下一个弹出的数字刚好是栈顶数字,那么直接弹出;如果下一个弹出的数字不在栈顶,则把压栈序列中还没有入栈的数字压入辅助栈,直到把下一个需要弹出的数字压入栈顶为止;如果所有数字都压入栈后仍然没有找到下一个弹出的数字,那么该序列不可能是一个弹出序列。
#include <stack>
bool IsPopOrder(const int* pPush, const int* pPop, int nLength)
{
bool bPossible = false;
if(pPush != nullptr && pPop != nullptr && nLength > 0)
{
const int* pNextPush = pPush;
const int* pNextPop = pPop;
std::stack<int> stackData;
while(pNextPop - pPop < nLength)
{
// 当辅助栈的栈顶元素不是要弹出的元素
// 先压入一些数字入栈
while(stackData.empty() || stackData.top() != *pNextPop)
{
// 如果所有数字都压入辅助栈了,退出循环
if(pNextPush - pPush == nLength)
break;
stackData.push(*pNextPush);
pNextPush ++;
}
if(stackData.top() != *pNextPop)
break;
stackData.pop();
pNextPop ++;
}
if(stackData.empty() && pNextPop - pPop == nLength)
bPossible = true;
}
return bPossible;
}
从上往下打印二叉树
题目:从上往下打印出二叉树的每个结点,同一层的结点按照从左到右的顺序打印。
思路:使用队列保存结点。
#include <deque>
void PrintFromTopToBottom(BinaryTreeNode* pRoot)
{
if(pRoot == nullptr)
return;
std::deque<BinaryTreeNode *> dequeTreeNode;
dequeTreeNode.push_back(pRoot);
while(dequeTreeNode.size())
{
BinaryTreeNode *pNode = dequeTreeNode.front();
dequeTreeNode.pop_front();
printf("%d ", pNode->m_nValue);
if(pNode->m_pLeft)
dequeTreeNode.push_back(pNode->m_pLeft);
if(pNode->m_pRight)
dequeTreeNode.push_back(pNode->m_pRight);
}
}
举一反三:不管是广度优先遍历一幅有向图还是一棵树,都要用到队列。首先把起始节点放入队列。接下来每次从队列的头部取出一个节点,遍历这个节点之后把它能到达的节点都一次放入队列。重复这个遍历过程,直到队列中的节点全部被遍历为止。
题目:从上到下按层打印二叉树,同一层的结点按从左到右的顺序打印,每一层打印到一行。
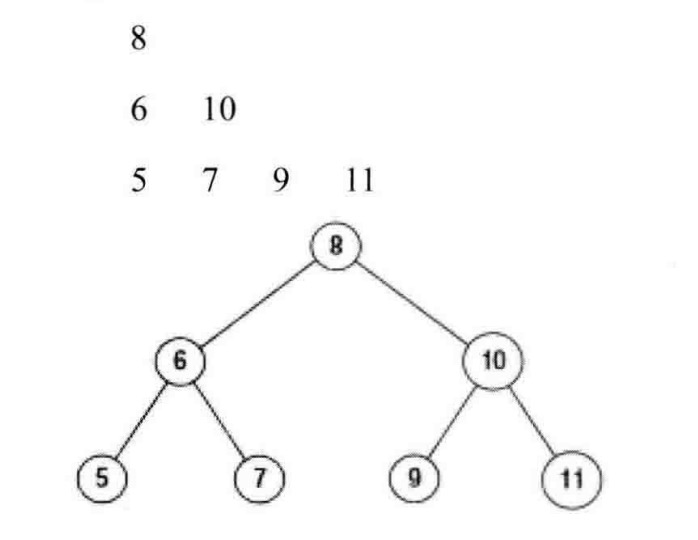
和前面的题类似,这里需要两个变量:一个变量表示在当前层中还没有打印的节点数;另一个变量表示下一层节点的数目。
#include <queue>
void Print(BinaryTreeNode* pRoot)
{
if(pRoot == nullptr)
return;
std::queue<BinaryTreeNode*> nodes;
nodes.push(pRoot);
int nextLevel = 0;
int toBePrinted = 1;
while(!nodes.empty())
{
BinaryTreeNode* pNode = nodes.front();
printf("%d ", pNode->m_nValue);
if(pNode->m_pLeft != nullptr)
{
nodes.push(pNode->m_pLeft);
++nextLevel;
}
if(pNode->m_pRight != nullptr)
{
nodes.push(pNode->m_pRight);
++nextLevel;
}
nodes.pop();
--toBePrinted;
if(toBePrinted == 0)
{
printf("\n");
toBePrinted = nextLevel;
nextLevel = 0;
}
}
}
题目:请实现一个函数按照之字形顺序打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右到左的顺序打印,第三行再按照从左到右的顺序打印,其他行以此类推。
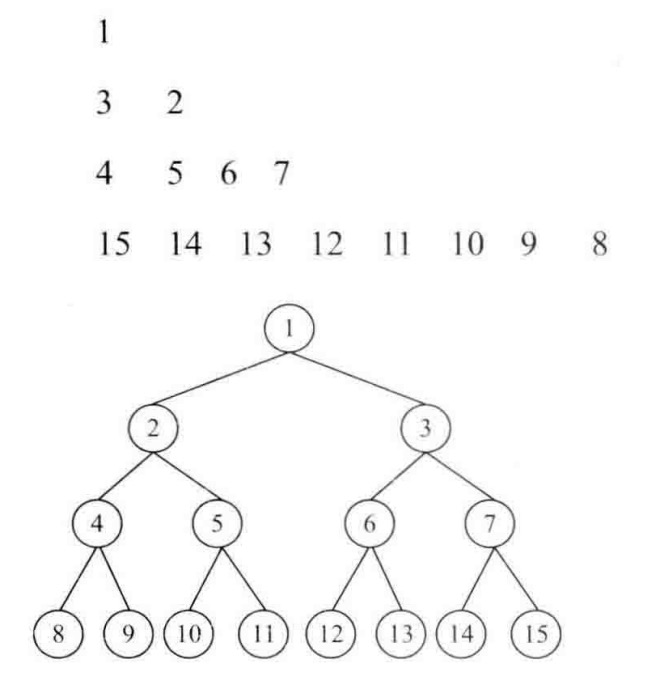
思路:按之字形顺序打印二叉树需要两个栈。我们在打印某一层的节点时,把下一层的子节点保存到相应的栈里。如果当前打印的是奇数层(第一层、第三层),则现保存左子节点再保存右子节点到第一个栈里;如果当前打印的是偶数层(第二层、第四层),则现保存右子节点再保存左子节点到第二个栈里。
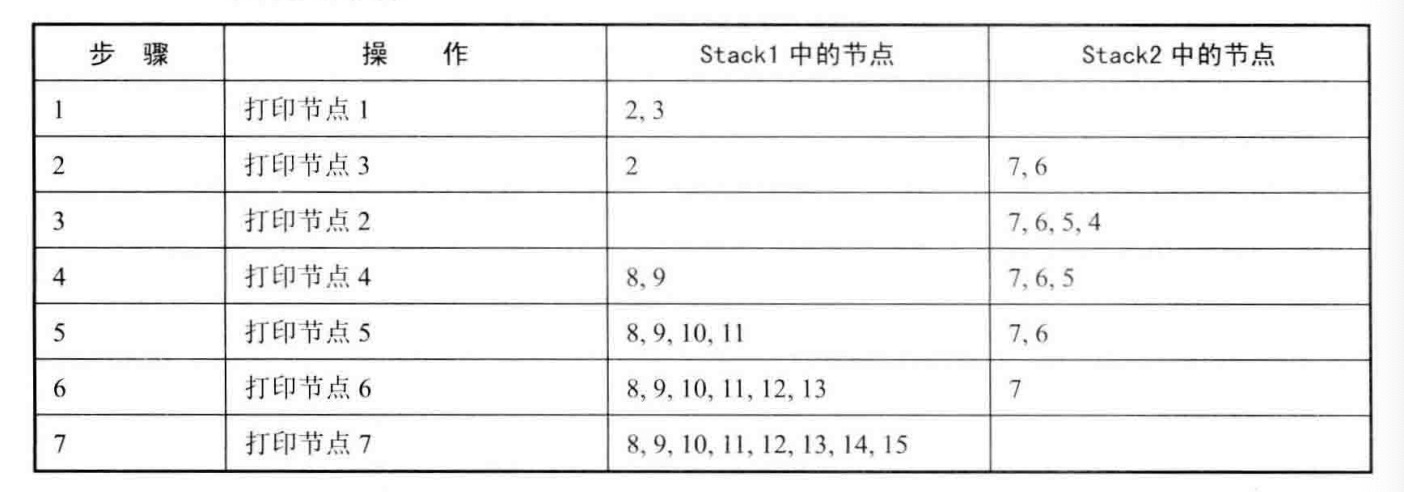
#include <stack>
void Print(BinaryTreeNode* pRoot)
{
if(pRoot == nullptr)
return;
std::stack<BinaryTreeNode*> levels[2];
int current = 0;
int next = 1;
levels[current].push(pRoot);
while(!levels[0].empty() || !levels[1].empty())
{
BinaryTreeNode* pNode = levels[current].top();
levels[current].pop();
printf("%d ", pNode->m_nValue);
if(current == 0)
{
if(pNode->m_pLeft != nullptr)
levels[next].push(pNode->m_pLeft);
if(pNode->m_pRight != nullptr)
levels[next].push(pNode->m_pRight);
}
else
{
if(pNode->m_pRight != nullptr)
levels[next].push(pNode->m_pRight);
if(pNode->m_pLeft != nullptr)
levels[next].push(pNode->m_pLeft);
}
if(levels[current].empty())
{
printf("\n");
current = 1 - current;
next = 1 - next;
}
}
}
二叉搜索树的后序遍历序列
题目:输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则返回true,否则返回false。假设输入的数组的任意两个数字都互不相同。例如,输入数组{5,7,6,9,11,10,8},则返回true,因为这个序列是下图二叉搜索树的后续遍历结果。如果输入的数组是{7,4,6,5},则由于没有哪颗二叉搜索树的后续遍历结果是这个序列,因此返回false。
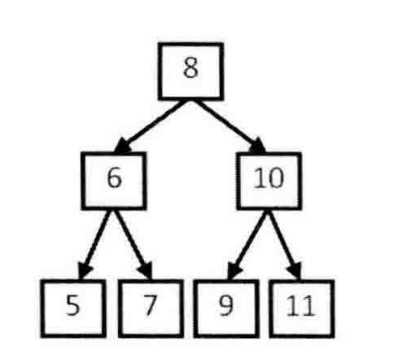
思路:在后序遍历得到的序列中,最后一个数字是树的根结点的值。数组中前面的数字可以分为两部分:第一部分是左子树的值,它们都比根节点小;第二部分是右子树的值,它们都比根结点的值大。接下来用同样的方法确定与数组每一步对应的子树的结构,这其实就是一个递归的过程。
// BST:Binary Search Tree,二叉搜索树
bool VerifySquenceOfBST(int sequence[], int length)
{
if(sequence == nullptr || length <= 0)
return false;
int root = sequence[length - 1];
// 在二叉搜索树中左子树的结点小于根结点
int i = 0;
for(; i < length - 1; ++ i)
{
if(sequence[i] > root)
break;
}
// 在二叉搜索树中右子树的结点大于根结点
int j = i;
for(; j < length - 1; ++ j)
{
if(sequence[j] < root)
return false;
}
// 判断左子树是不是二叉搜索树
bool left = true;
if(i > 0)
left = VerifySquenceOfBST(sequence, i);
// 判断右子树是不是二叉搜索树
bool right = true;
if(i < length - 1)
right = VerifySquenceOfBST(sequence + i, length - i - 1);
return (left && right);
}
相关题目:输入一个整数数组,判断该数组是不是某二叉搜索树的前序遍历结果。这个前面问题的后序遍历很类似,只是在前序遍历的序列中,第一个数字是根结点的值。
举一反三:如果面试题要求处理一颗二叉树的遍历序列,则可以先找到二叉树的根结点,再基于根结点把整棵树的遍历序列拆分成左子树对应的子序列和右子树对应的子序列,接下来再递归处理这两个子序列。
二叉树中和为某一值的路径
题目:输入一棵二叉树和一个整数,打印出二叉树中结点值的和为输入整数的所有路径。从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。
#include <vector>
void FindPath(BinaryTreeNode* pRoot, int expectedSum, std::vector<int>& path, int& currentSum);
void FindPath(BinaryTreeNode* pRoot, int expectedSum)
{
if(pRoot == nullptr)
return;
std::vector<int> path;
int currentSum = 0;
FindPath(pRoot, expectedSum, path, currentSum);
}
void FindPath
(
BinaryTreeNode* pRoot,
int expectedSum,
std::vector<int>& path,
int& currentSum
)
{
currentSum += pRoot->m_nValue;
path.push_back(pRoot->m_nValue);
// 如果是叶结点,并且路径上结点的和等于输入的值
// 打印出这条路径
bool isLeaf = pRoot->m_pLeft == nullptr && pRoot->m_pRight == nullptr;
if(currentSum == expectedSum && isLeaf)
{
printf("A path is found: ");
std::vector<int>::iterator iter = path.begin();
for(; iter != path.end(); ++ iter)
printf("%d\t", *iter);
printf("\n");
}
// 如果不是叶结点,则遍历它的子结点
if(pRoot->m_pLeft != nullptr)
FindPath(pRoot->m_pLeft, expectedSum, path, currentSum);
if(pRoot->m_pRight != nullptr)
FindPath(pRoot->m_pRight, expectedSum, path, currentSum);
// 在返回到父结点之前,在路径上删除当前结点,
// 并在currentSum中减去当前结点的值
currentSum -= pRoot->m_nValue;
path.pop_back();
}
复杂链表的复制
题目:请实现函数ComplexListNode* Clone(ComplexListNode* pHead),复制一个复杂链表。在复杂链表中,每个结点除了有一个m_pNext指针指向下一个结点外,还有一个m_pSibling 指向链表中的任意结点或者nullptr。
struct ComplexListNode
{
int m_nValue;
ComplexListNode* m_pNext;
ComplexListNode* m_pSibling;
};
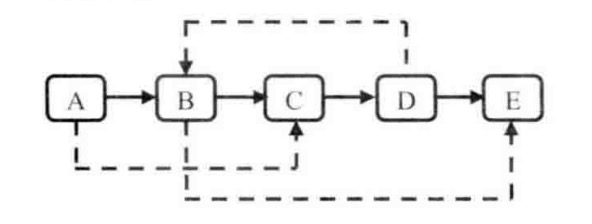
思路1:第一步复制原始链表上的每个节点N创建N’,然后把这些创建出来的节点连接起来。同时我们把<N,N'>的配对信息放到一个哈希表中。第二步设置链表上每个节点的m_pSibling。如果在原始链表中节点N的m_pSibling指向节点S,那么在复制链表中,对应的N’应该指向S’。由于有了哈希表,我们可以用O(1)的时间根据S找到S’。
思路2:
第一步根据原始链表每个节点N创建对应的N’。这一次,我们把N’链接在N的后面。
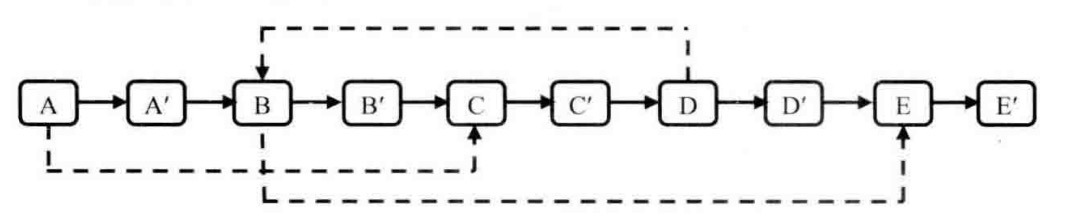
第二步设置复制出来的节点的m_pSibling。假设原始链表上的N的m_pSibling指向节点S,那么其对应复制出来的N’是N的m_pNext指向的节点,同样S’也是S的m_pNext指向的节点。
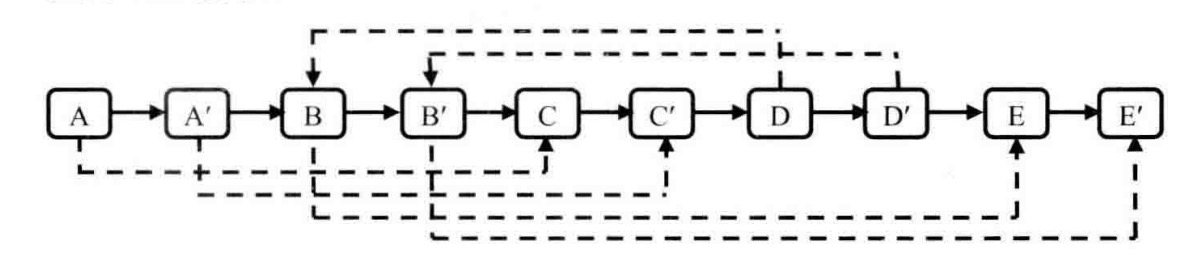
第三步把这个长链表拆分成两个链表:把奇数位置的节点用m_pNext链接起来就是原始链表,把偶数位置的节点用m_pNext链接起来就是复制出来的链表。
#include "ComplexList.h"
void CloneNodes(ComplexListNode* pHead);
void ConnectSiblingNodes(ComplexListNode* pHead);
ComplexListNode* ReconnectNodes(ComplexListNode* pHead);
ComplexListNode* Clone(ComplexListNode* pHead)
{
CloneNodes(pHead);
ConnectSiblingNodes(pHead);
return ReconnectNodes(pHead);
}
void CloneNodes(ComplexListNode* pHead)
{
ComplexListNode* pNode = pHead;
while(pNode != nullptr)
{
ComplexListNode* pCloned = new ComplexListNode();
pCloned->m_nValue = pNode->m_nValue;
pCloned->m_pNext = pNode->m_pNext;
pCloned->m_pSibling = nullptr;
pNode->m_pNext = pCloned;
pNode = pCloned->m_pNext;
}
}
void ConnectSiblingNodes(ComplexListNode* pHead)
{
ComplexListNode* pNode = pHead;
while(pNode != nullptr)
{
ComplexListNode* pCloned = pNode->m_pNext;
if(pNode->m_pSibling != nullptr)
{
pCloned->m_pSibling = pNode->m_pSibling->m_pNext;
}
pNode = pCloned->m_pNext;
}
}
ComplexListNode* ReconnectNodes(ComplexListNode* pHead)
{
ComplexListNode* pNode = pHead;
ComplexListNode* pClonedHead = nullptr;
ComplexListNode* pClonedNode = nullptr;
if(pNode != nullptr)
{
pClonedHead = pClonedNode = pNode->m_pNext;
pNode->m_pNext = pClonedNode->m_pNext;
pNode = pNode->m_pNext;
}
while(pNode != nullptr)
{
pClonedNode->m_pNext = pNode->m_pNext;
pClonedNode = pClonedNode->m_pNext;
pNode->m_pNext = pClonedNode->m_pNext;
pNode = pNode->m_pNext;
}
return pClonedHead;
}
二叉搜索树与双向链表
题目:输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点,只能调整树中结点指针的指向。
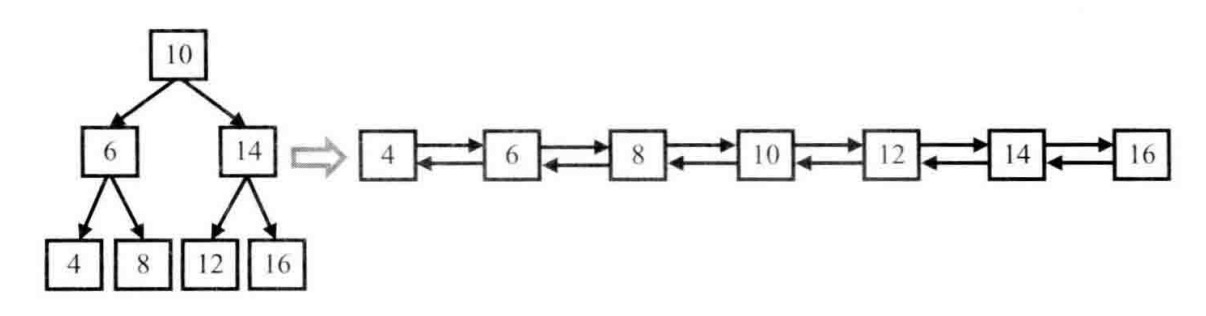
把二叉搜索树看出3部分,根结点、左子树、右子树。在吧左、右子树都转换成排序双向链表之后再和根结点链接起来,整棵二叉搜索树也就转换成了排序双向链表。
void ConvertNode(BinaryTreeNode* pNode, BinaryTreeNode** pLastNodeInList);
BinaryTreeNode* Convert(BinaryTreeNode* pRootOfTree)
{
BinaryTreeNode *pLastNodeInList = nullptr;
ConvertNode(pRootOfTree, &pLastNodeInList);
// pLastNodeInList指向双向链表的尾结点,
// 我们需要返回头结点
BinaryTreeNode *pHeadOfList = pLastNodeInList;
while(pHeadOfList != nullptr && pHeadOfList->m_pLeft != nullptr)
pHeadOfList = pHeadOfList->m_pLeft;
return pHeadOfList;
}
void ConvertNode(BinaryTreeNode* pNode, BinaryTreeNode** pLastNodeInList)
{
if(pNode == nullptr)
return;
BinaryTreeNode *pCurrent = pNode;
if (pCurrent->m_pLeft != nullptr)
ConvertNode(pCurrent->m_pLeft, pLastNodeInList);
pCurrent->m_pLeft = *pLastNodeInList;
if(*pLastNodeInList != nullptr)
(*pLastNodeInList)->m_pRight = pCurrent;
*pLastNodeInList = pCurrent;
if (pCurrent->m_pRight != nullptr)
ConvertNode(pCurrent->m_pRight, pLastNodeInList);
}
序列化二叉树
题目:请实现两个函数,分别用来序列化和反序列化二叉树。
思路:我们可以根据前序遍历的顺序来序列化二叉树,因为前序遍历是从根节点开始的。在遍历二叉树碰到nullptr指针时,这些指针序列化为一个特殊的字符(如’$’)。

#include <iostream>
#include <fstream>
using namespace std;
void Serialize(const BinaryTreeNode* pRoot, ostream& stream)
{
if(pRoot == nullptr)
{
stream << "$,";
return;
}
stream << pRoot->m_nValue << ',';
Serialize(pRoot->m_pLeft, stream);
Serialize(pRoot->m_pRight, stream);
}
bool ReadStream(istream& stream, int* number)
{
if(stream.eof())
return false;
char buffer[32];
buffer[0] = '\0';
char ch;
stream >> ch;
int i = 0;
while(!stream.eof() && ch != ',')
{
buffer[i++] = ch;
stream >> ch;
}
bool isNumeric = false;
if(i > 0 && buffer[0] != '$')
{
*number = atoi(buffer);
isNumeric = true;
}
return isNumeric;
}
void Deserialize(BinaryTreeNode** pRoot, istream& stream)
{
int number;
if(ReadStream(stream, &number))
{
*pRoot = new BinaryTreeNode();
(*pRoot)->m_nValue = number;
(*pRoot)->m_pLeft = nullptr;
(*pRoot)->m_pRight = nullptr;
Deserialize(&((*pRoot)->m_pLeft), stream);
Deserialize(&((*pRoot)->m_pRight), stream);
}
}
字符串的排列
题目:输入一个字符串,打印出该字符串中字符的所有排列。例如输入字符串abc,则打印出由字符a、b、c所能排列出来的所有字符串abc、acb、bac、bca、cab和cba。
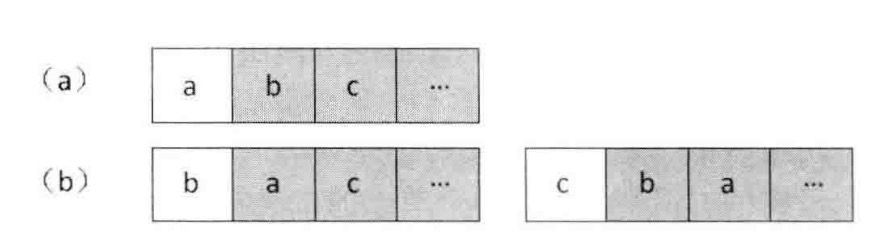
思路:1. 把字符串分为两部分:一部分是字符串的第一个字符;另一部分是第一个字符以后的所有字符。接下来求阴影部分的字符串排列。2. 每次拿第一个字符和它后面的字符逐个交换。
void Permutation(char* pStr, char* pBegin);
void Permutation(char* pStr)
{
if(pStr == nullptr)
return;
Permutation(pStr, pStr);
}
void Permutation(char* pStr, char* pBegin)
{
if(*pBegin == '\0')
{
printf("%s\n", pStr);
}
else
{
for(char* pCh = pBegin; *pCh != '\0'; ++ pCh)
{
char temp = *pCh;
*pCh = *pBegin;
*pBegin = temp;
Permutation(pStr, pBegin + 1);
temp = *pCh;
*pCh = *pBegin;
*pBegin = temp;
}
}
}
本题拓展:如果不是求字符的所有排列,而是求字符的所有组合,应该怎么办呢?还是输入三个字符a、b、c,则它们的组合有a、b、c、ab、ac、bc、abc。当交换字符串中的两个字符时,虽然能得到两个不同的排列,但却是同一个组合。比如ab和ba是不同的排列,但只算一个组合。
如果输入n个字符,则这n个字符能够构成长度为1,2,…n的组合。在求n个字符的长度为m(1<=m<=n)的组合的时候,我们把这n个字符分成两部分:第一个字符和其余的所有字符。如果组合里包含第一个字符,则下一步在剩余的字符里选取m-1个字符;如果组合里不包括第一个字符,则下一步在剩余的n-1个字符里选取m个字符。也就是说,我们可以把求n个字符组成长度为m的组合的问题分解成两个子问题,分别求n-1个字符中长度为m-1的组合,以及求n-1个字符中长度为m的组合。这两个子问题都可以用递归的方式解决。
相关题目:
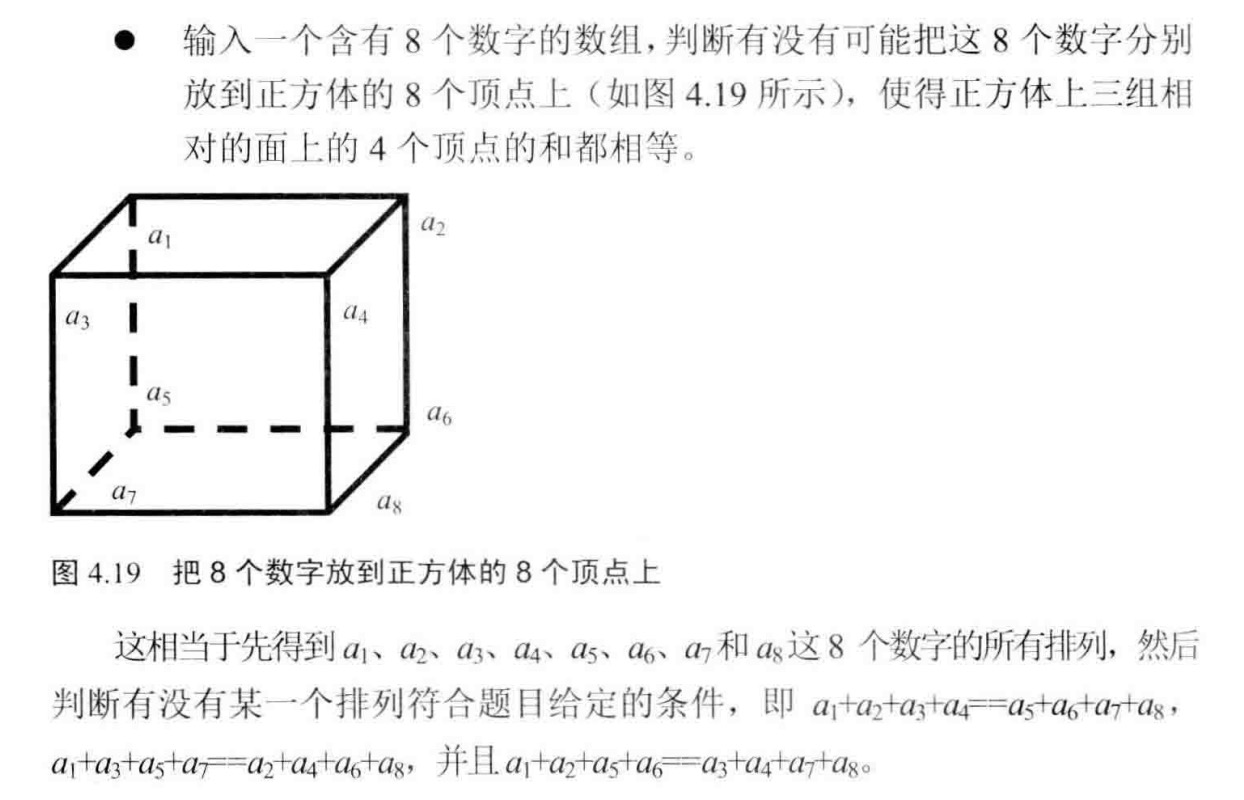


举一反三:如果面试题是按照一定要求摆放若干个数字,则可以先求出这些数字的所有排列,然后一一判断每个排列是不是满足题目给定的要求。
数组中出现次数超过一半的数字
题目:数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。例如输入一个长度为9的数组{1, 2, 3, 2, 2, 2, 5, 4, 2}。由于数字2在数组中出现了5次,超过数组长度的一半,因此输出2。
解法一:基于partition函数的时间复杂度为O(n)的算法
如果把这个数组排序,那么排序之后位于数组中间的数字一定就是那个出现次数超过数组长度一半的数字。也就是说,这个数字就是长度为n的数组中第n/2大的数字。我们有成熟的时间复杂度为O(n)的算法得到数组中任意第k大的数字。
这种算法受快速排序算法的启发。如果这个选中的数字的下标刚好是n/2,那么这个数字就是数组的中位数。如果它的下标大于n/2,那么中位数应该位于他的左边,我们可以接着在它的左边部分的数组中查找;如果它的下标小于n/2,那么中位数应该位于他的右边,我们可以接着在它右边部分的数组中查找;这是一个典型的递归过程。
解法二:根据数组特点找出时间复杂度为O(n)的算法
我们可以在遍历数组的时候保存两个值:一个是数组的一个数字;另一个是次数。由于我们要找的数字出现的次数比其他所以数字出现的次数之和还要多,那么要找的数字就是最后一次把次数设为1时对应的数字。
bool g_bInputInvalid = false;
bool CheckInvalidArray(int* numbers, int length)
{
g_bInputInvalid = false;
if(numbers == nullptr && length <= 0)
g_bInputInvalid = true;
return g_bInputInvalid;
}
bool CheckMoreThanHalf(int* numbers, int length, int number)
{
int times = 0;
for(int i = 0; i < length; ++i)
{
if(numbers[i] == number)
times++;
}
bool isMoreThanHalf = true;
if(times * 2 <= length)
{
g_bInputInvalid = true;
isMoreThanHalf = false;
}
return isMoreThanHalf;
}
// ====================方法1====================
int MoreThanHalfNum_Solution1(int* numbers, int length)
{
if(CheckInvalidArray(numbers, length))
return 0;
int middle = length >> 1;
int start = 0;
int end = length - 1;
int index = Partition(numbers, length, start, end);
while(index != middle)
{
if(index > middle)
{
end = index - 1;
index = Partition(numbers, length, start, end);
}
else
{
start = index + 1;
index = Partition(numbers, length, start, end);
}
}
int result = numbers[middle];
if(!CheckMoreThanHalf(numbers, length, result))
result = 0;
return result;
}
// ====================方法2====================
int MoreThanHalfNum_Solution2(int* numbers, int length)
{
if(CheckInvalidArray(numbers, length))
return 0;
int result = numbers[0];
int times = 1;
for(int i = 1; i < length; ++i)
{
if(times == 0)
{
result = numbers[i];
times = 1;
}
else if(numbers[i] == result)
times++;
else
times--;
}
if(!CheckMoreThanHalf(numbers, length, result))
result = 0;
return result;
}
最小的k个数
题目:输入n个整数,找出其中最小的k个数。例如输入4、5、1、6、2、7、3、8这8个数字,则最小的4个数字是1、2、3、4。
解法一:基于partition函数的时间复杂度为O(n)的算法,只有当我们可以修改输入的数组时可用
如果基于数组的第k个数字来调整,则使得比第k个数字小的所有数字都位于数组的左边,比第k个数字大的所有数字都位于数组右边。这样调整之后,位于数组左边的k个数字就是最小的k个数字(这k个数字不一定是排序的)
解法二:时间复杂度为O(nlogk)的算法,特别适合处理海量数据
我们可以先创建一个大小为k的数据容器来储存最小的k个数字,接下来每次从输入的n个整数中读入一个数。如果容器中已有的数字少于k个,则直接放入;如果容器中已有k个数字,也就是容器已满,此时需要找出已有的k个树中的最大值,然后拿这次待插入的整数和最大值进行比较。如果待插入的值比当前已有的最大值小,则用这个数替换当前已有的最大值;如果待插入的值比当前已有的最大值还要大,那么这个数不可能时最小的k个整数之一,于是我们可以抛弃这个整数。
我们可以使用最大堆来实现这个数据容器,每次可以在O(1)时间内得到已有的k个数字中的最大值,但需要O(logk)时间完成删除以及插入操作。我们还可以采用红黑树来实现我们的容器,红黑树通过把节点分为红、黑两种颜色并根据一些规则确保树在一定程度上是平衡的,从而保证在红黑树中的查找、删除、插入操作都只需要O(logk)时间。在STL中,set和multiset都是基于红黑树实现的。
#include <set>
#include <vector>
using namespace std;
// ====================方法1====================
void GetLeastNumbers_Solution1(int* input, int n, int* output, int k)
{
if(input == nullptr || output == nullptr || k > n || n <= 0 || k <= 0)
return;
int start = 0;
int end = n - 1;
int index = Partition(input, n, start, end);
while(index != k - 1)
{
if(index > k - 1)
{
end = index - 1;
index = Partition(input, n, start, end);
}
else
{
start = index + 1;
index = Partition(input, n, start, end);
}
}
for(int i = 0; i < k; ++i)
output[i] = input[i];
}
// ====================方法2====================
typedef multiset<int, std::greater<int> > intSet;
typedef multiset<int, std::greater<int> >::iterator setIterator;
void GetLeastNumbers_Solution2(const vector<int>& data, intSet& leastNumbers, int k)
{
leastNumbers.clear();
if(k < 1 || data.size() < k)
return;
vector<int>::const_iterator iter = data.begin();
for(; iter != data.end(); ++ iter)
{
if((leastNumbers.size()) < k)
leastNumbers.insert(*iter);
else
{
setIterator iterGreatest = leastNumbers.begin();
if(*iter < *(leastNumbers.begin()))
{
leastNumbers.erase(iterGreatest);
leastNumbers.insert(*iter);
}
}
}
}
第二种解法虽然慢一点,但它有两个明显的优点。一是没有修改输入的数据。而是该算法适合海量数据的输入。假设题目要求从海量的数据中找出最小的k个数字,由于内存大小是有限的,有可能不能把这些海量的数据一次性全部载入内存。这个时候,我们可以从辅助储存空间(如硬盘)中每次读入一个数字,这种思路只要求内存能够容纳leastNumbers即可,因此他最适合的情形就是n很大并且k较小的问题。
数据流中的中位数
题目:如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。
思路:
未排序数组:使用partition函数找出数组中位数。插入只需O(1)
排序数组:插入需要O(n),找吹中位数只需O(1)
排序链表:插入需要O(n)。定义两个指针指向链表中间的节点(如果链表的节点数目是奇数,那么这两个指针指向同一个节点),那么可以在O(1)时间内得出中位数
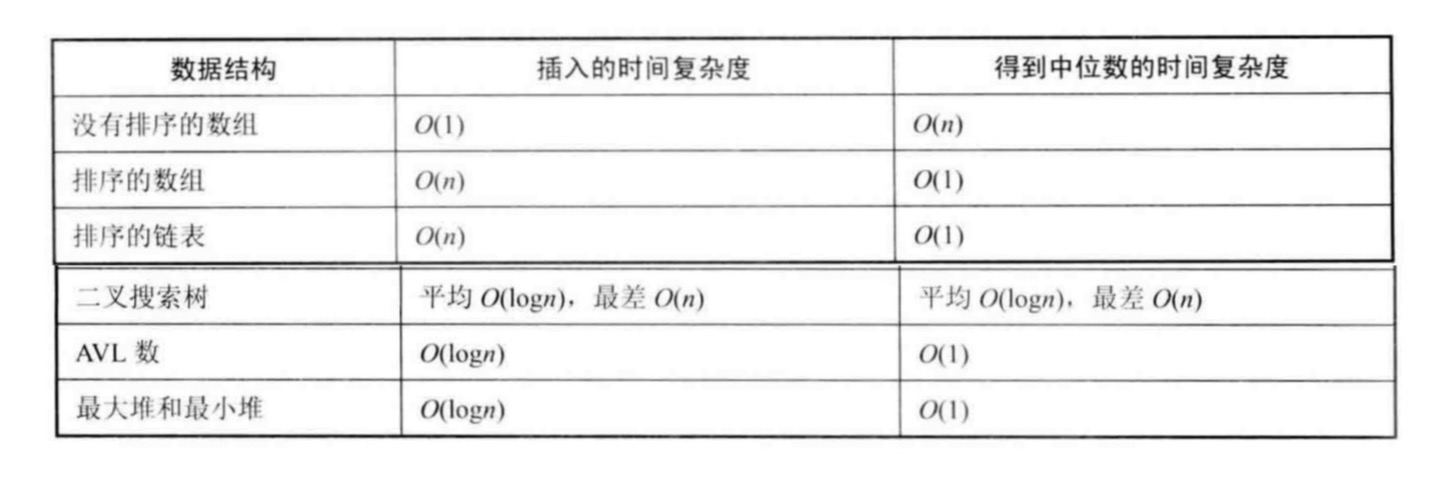
二叉搜索树:插入新数据平均时间降低到O(logn)。但是当二叉搜索树极度不平衡从而看起来像一个排序链表时,插入新数据的时间仍然是O(n)。为了得到中位数,可以在二叉树节点中添加一个表示子树节点数目的字段。有了这个字段,可以在平均O(logn)时间内得到中位数,但最差情况仍然需要O(n)
AVL树:为了避免二叉搜索树的最差情况,可以利用平衡的二叉搜索树,即AVL树。通常AVL树的平衡因子是左、右子树的高度差。可以稍作修改,把AVL的平衡因子改为左、右子树节点数目之差。有了这个改动,可以用O(logn)时间往AVL树中添加一个新节点,同时用O(1)时间得到所有节点的中位数。
最大堆和最小堆:用一个最大堆实现左边的数据容器,用一个最小堆实现右边的数据容器。往堆中插入一个数据堆时间效率是O(logn)。由于只需要O(1)时间就可以得到位于堆顶的数据,因此得到中位数的时间复杂度是O(1)。
using namespace std;
template<typename T> class DynamicArray
{
public:
void Insert(T num)
{
if(((min.size() + max.size()) & 1) == 0)
{
if(max.size() > 0 && num < max[0])
{
max.push_back(num);
push_heap(max.begin(), max.end(), less<T>());
num = max[0];
pop_heap(max.begin(), max.end(), less<T>());
max.pop_back();
}
min.push_back(num);
push_heap(min.begin(), min.end(), greater<T>());
}
else
{
if(min.size() > 0 && min[0] < num)
{
min.push_back(num);
push_heap(min.begin(), min.end(), greater<T>());
num = min[0];
pop_heap(min.begin(), min.end(), greater<T>());
min.pop_back();
}
max.push_back(num);
push_heap(max.begin(), max.end(), less<T>());
}
}
T GetMedian()
{
int size = min.size() + max.size();
if(size == 0)
throw exception("No numbers are available");
T median = 0;
if((size & 1) == 1)
median = min[0];
else
median = (min[0] + max[0]) / 2;
return median;
}
private:
vector<T> min;
vector<T> max;
};
连续子数组的最大和
题目:输入一个整型数组,数组里有正数也有负数。数组中一个或连续的多个整数组成一个子数组。求所有子数组的和的最大值。要求时间复杂度为O(n)。
解法一:举例分析数组的规律,使用两个变量:一个保存当前子数组的和,一个保存得到过的最大和。
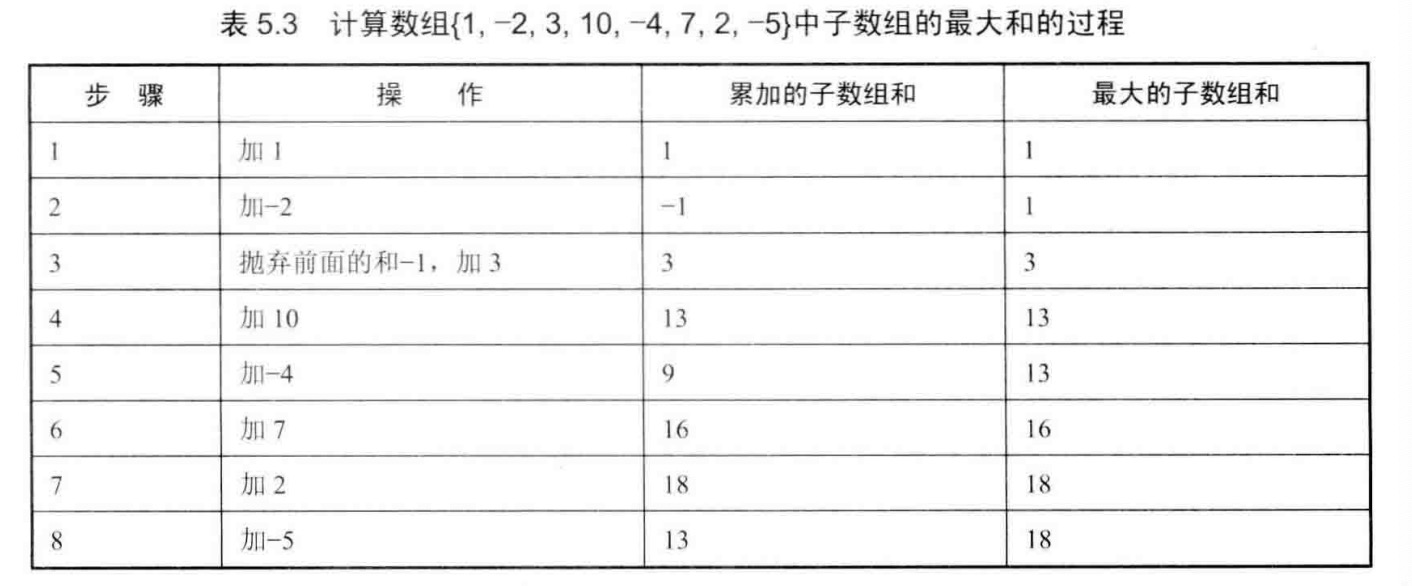
解法二:应用动态规划法,如果用函数f(i)表示以第i个数字结尾的子数组的最大和,那么我们需要求出max[f(i)],其中0<=i<n。我们可以用如下递归公式求f(i):

bool g_InvalidInput = false;
int FindGreatestSumOfSubArray(int *pData, int nLength)
{
if((pData == nullptr) || (nLength <= 0))
{
g_InvalidInput = true;
return 0;
}
g_InvalidInput = false;
int nCurSum = 0;
int nGreatestSum = 0x80000000;
for(int i = 0; i < nLength; ++i)
{
if(nCurSum <= 0)
nCurSum = pData[i];
else
nCurSum += pData[i];
if(nCurSum > nGreatestSum)
nGreatestSum = nCurSum;
}
return nGreatestSum;
}
从1到n整数中1出现的次数
题目:输入一个整数n,求从1到n这n个整数的十进制表示中1出现的次数。例如输入12,从1到12这些整数中包含1 的数字有1,10,11和12,1一共出现了5次。
// ====================方法一====================
int NumberOf1(unsigned int n);
int NumberOf1Between1AndN_Solution1(unsigned int n)
{
int number = 0;
for(unsigned int i = 1; i <= n; ++ i)
number += NumberOf1(i);
return number;
}
int NumberOf1(unsigned int n)
{
int number = 0;
while(n)
{
if(n % 10 == 1)
number ++;
n = n / 10;
}
return number;
}
// ====================方法二====================
int NumberOf1(const char* strN);
int PowerBase10(unsigned int n);
int NumberOf1Between1AndN_Solution2(int n)
{
if(n <= 0)
return 0;
char strN[50];
sprintf(strN, "%d", n);
return NumberOf1(strN);
}
int NumberOf1(const char* strN)
{
if(!strN || *strN < '0' || *strN > '9' || *strN == '\0')
return 0;
int first = *strN - '0';
unsigned int length = static_cast<unsigned int>(strlen(strN));
if(length == 1 && first == 0)
return 0;
if(length == 1 && first > 0)
return 1;
// 假设strN是"21345"
// numFirstDigit是数字10000-19999的第一个位中1的数目
int numFirstDigit = 0;
if(first > 1)
numFirstDigit = PowerBase10(length - 1);
else if(first == 1)
numFirstDigit = atoi(strN + 1) + 1;
// numOtherDigits是01346-21345除了第一位之外的数位中1的数目
int numOtherDigits = first * (length - 1) * PowerBase10(length - 2);
// numRecursive是1-1345中1的数目
int numRecursive = NumberOf1(strN + 1);
return numFirstDigit + numOtherDigits + numRecursive;
}
int PowerBase10(unsigned int n)
{
int result = 1;
for(unsigned int i = 0; i < n; ++ i)
result *= 10;
return result;
}
数字序列中某一位的数字
题目:数字以0123456789101112131415…的格式序列化到一个字符序列中。在这个序列中,第5位(从0开始计数)是5,第13位是1,第19位是4,等等。请写一个函数求任意位对应的数字。

int countOfIntegers(int digits);
int digitAtIndex(int index, int digits);
int beginNumber(int digits);
int digitAtIndex(int index)
{
if(index < 0)
return -1;
int digits = 1;
while(true)
{
int numbers = countOfIntegers(digits);
if(index < numbers * digits)
return digitAtIndex(index, digits);
index -= digits * numbers;
digits++;
}
return -1;
}
int countOfIntegers(int digits)
{
if(digits == 1)
return 10;
int count = (int) std::pow(10, digits - 1);
return 9 * count;
}
int digitAtIndex(int index, int digits)
{
int number = beginNumber(digits) + index / digits;
int indexFromRight = digits - index % digits;
for(int i = 1; i < indexFromRight; ++i)
number /= 10;
return number % 10;
}
int beginNumber(int digits)
{
if(digits == 1)
return 0;
return (int) std::pow(10, digits - 1);
}
把数组排成最小的数
题目:输入一个正整数数组,把数组里所有数字拼接起来排成一个数,打印能拼接出的所有数字中最小的一个。例如输入数组{3, 32, 321},则打印出这3个数字能排成的最小数字321323。
这里其实是希望我们能找到一个排序规则,数组根据这个规则排序后能排成一个最小的数字。要确定排序规则,就要比较两个数字,也就是给出两个数字m和n,我们需要确定一个规则判断m和n那个哪个应该排在前面,而不是仅仅比较这两个数字哪个更大。
按题目的要求,两个数字m和n能拼接成数字mn和nm。如果mn<nm,那么我们应该打印出mn,也就是m应该排在n的前面,我们定义此时m小于n;
接下来考虑怎么去拼接数字,即给出数字m和n,怎么得到数字mn和nm并比较它们的大小。需要考虑m和n都在int型能表达的范围内,但把它们拼接起来的数字mn和nm用int型表示就有可能溢出了,所以这还是一个隐形的大数问题。
一个非常直观的解决方法就是把数字转换成字符串,另外,由于把数字m和n拼接起来得到mn和nm,它们的位数肯定是相同的,因此比较它们的大小只需要按照字符串大小的比较规则就可以了。
int compare(const void* strNumber1, const void* strNumber2);
// int型整数用十进制表示最多只有10位
const int g_MaxNumberLength = 10;
char* g_StrCombine1 = new char[g_MaxNumberLength * 2 + 1];
char* g_StrCombine2 = new char[g_MaxNumberLength * 2 + 1];
void PrintMinNumber(const int* numbers, int length)
{
if(numbers == nullptr || length <= 0)
return;
char** strNumbers = (char**)(new int[length]);
for(int i = 0; i < length; ++i)
{
strNumbers[i] = new char[g_MaxNumberLength + 1];
sprintf(strNumbers[i], "%d", numbers[i]);
}
qsort(strNumbers, length, sizeof(char*), compare);
for(int i = 0; i < length; ++i)
printf("%s", strNumbers[i]);
printf("\n");
for(int i = 0; i < length; ++i)
delete[] strNumbers[i];
delete[] strNumbers;
}
// 如果[strNumber1][strNumber2] > [strNumber2][strNumber1], 返回值大于0
// 如果[strNumber1][strNumber2] = [strNumber2][strNumber1], 返回值等于0
// 如果[strNumber1][strNumber2] < [strNumber2][strNumber1], 返回值小于0
int compare(const void* strNumber1, const void* strNumber2)
{
// [strNumber1][strNumber2]
strcpy(g_StrCombine1, *(const char**)strNumber1);
strcat(g_StrCombine1, *(const char**)strNumber2);
// [strNumber2][strNumber1]
strcpy(g_StrCombine2, *(const char**)strNumber2);
strcat(g_StrCombine2, *(const char**)strNumber1);
return strcmp(g_StrCombine1, g_StrCombine2);
}
把数字翻译成字符串
题目:给定一个数字,我们按照如下规则把它翻译为字符串:0翻译成”a”,1翻译成”b”,……,11翻译成”l”,……,25翻译成”z”。一个数字可能有多个翻译。例如12258有5种不同的翻译,它们分别是”bccfi”、”bwfi”、”bczi”、”mcfi”和”mzi”。请编程实现一个函数用来计算一个数字有多少种不同的翻译方法。
思路:我们定义函数f(i)表示从第i位数字开始的不同翻译的数目,那么f(i)=f(i+1)+g(i,i+1)*f(i+2),当第i位和第i+1位数字拼接起来的数字在10~25的范围内时,函数g(i,i+1)的值为1;否则为0.
尽管我们使用递归的思路来分析这个问题,但由于存在重复的子问题,递归并不是解决这个问题的最佳方法。递归是从最大的文推开始自上而下解决问题,我们也可以从最小的子问题开始自下而上解决问题,这样就可以消除重复的子问题。也就是说,我们从数字的末尾开始,然后从右到左翻译并计算不同翻译的数目。
int GetTranslationCount(const string& number);
int GetTranslationCount(int number)
{
if(number < 0)
return 0;
string numberInString = to_string(number);
return GetTranslationCount(numberInString);
}
int GetTranslationCount(const string& number)
{
int length = number.length();
int* counts = new int[length];
int count = 0;
for(int i = length - 1; i >= 0; --i)
{
count = 0;
if(i < length - 1)
count = counts[i + 1];
else
count = 1;
if(i < length - 1)
{
int digit1 = number[i] - '0';
int digit2 = number[i + 1] - '0';
int converted = digit1 * 10 + digit2;
if(converted >= 10 && converted <= 25)
{
if(i < length - 2)
count += counts[i + 2];
else
count += 1;
}
}
counts[i] = count;
}
count = counts[0];
delete[] counts;
return count;
}
礼物的最大价值
题目:在一个m×n的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于0)。你可以从棋盘的左上角开始拿格子里的礼物,并每次向左或者向下移动一格直到到达棋盘的右下角。给定一个棋盘及其上面的礼物,请计算你最多能拿到多少价值的礼物?

思路:这是一个典型的能用动态规划解决的问题。我们先用递归的思路来分析。定义一个函数f(i,j)表示到达坐标(i,j)的格子时能拿到的礼物总和的最大值。有两种可能的途径达到坐标为(i,j)的格子:f(i,j)=max(f(i-1,j),f(i,j-1))+gift[i,j]。gift[i,j]表示坐标为(i,j)的格子里礼物的价值。
依旧,递归分析,循环写代码。为了缓存中间计算结果,我们需要一个辅助的二维数组。数组中坐标为(i,j)的元素表示到达坐标(i,j)的格子时能拿到的礼物价值总和的最大值。
优化:到达坐标为(i,j)的格子时能够拿到的礼物的最大价值只依赖坐标为(i-1,j)和(i,j-1)的两个格子,因此第i-2行及更上面的所有格子的最大价值实际上没有必要保存下来。我们可以用一个一维数组来代替二维矩阵。
int getMaxValue_solution1(const int* values, int rows, int cols)
{
if(values == nullptr || rows <= 0 || cols <= 0)
return 0;
int** maxValues = new int*[rows];
for(int i = 0; i < rows; ++i)
maxValues[i] = new int[cols];
for(int i = 0; i < rows; ++i)
{
for(int j = 0; j < cols; ++j)
{
int left = 0;
int up = 0;
if(i > 0)
up = maxValues[i - 1][j];
if(j > 0)
left = maxValues[i][j - 1];
maxValues[i][j] = std::max(left, up) + values[i * cols + j];
}
}
int maxValue = maxValues[rows - 1][cols - 1];
for(int i = 0; i < rows; ++i)
delete[] maxValues[i];
delete[] maxValues;
return maxValue;
}
int getMaxValue_solution2(const int* values, int rows, int cols)
{
if(values == nullptr || rows <= 0 || cols <= 0)
return 0;
int* maxValues = new int[cols];
for(int i = 0; i < rows; ++i)
{
for(int j = 0; j < cols; ++j)
{
int left = 0;
int up = 0;
if(i > 0)
up = maxValues[j];
if(j > 0)
left = maxValues[j - 1];
maxValues[j] = std::max(left, up) + values[i * cols + j];
}
}
int maxValue = maxValues[cols - 1];
delete[] maxValues;
return maxValue;
}
最长不含重复字符的子字符串
题目:请从字符串中找出一个最长的不包含重复字符的子字符串,计算该最长子字符串的长度。假设字符串中只包含从’a’到’z’的字符。
思路:使用动态规划算法来提高效率。首先定义函数f(i)表示以第i个字符为结尾的不包含重复字符的子字符串的最长长度。我们从左到右逐一扫描字符串中的每个字符。
如果第i个字符之前没有出现过,那么f(i)=f(i-1)+1。
如果第i个字符之前出现过,那么情况就要复杂一点了。我们先计算第i个字符和它上次出现在字符串中的位置的距离,并记为d,接着分两种情形分析。第一种情形是d小于或者等于f(i-1),此时第i个字符上次出现在f(i-1)对应的最长子字符串之中,因此f(i)=d。
第二种情形是d大于f(i-1),此时第i个字符上次出现在f(i-1)对应的最长字符串之前,因此仍然有f(i)=f(i-1)+1。
// 方法一:蛮力法
bool hasDuplication(const std::string& str, int position[]);
int longestSubstringWithoutDuplication_1(const std::string& str)
{
int longest = 0;
int* position = new int[26];
for(int start = 0; start < str.length(); ++start)
{
for(int end = start; end < str.length(); ++end)
{
int count = end - start + 1;
const std::string& substring = str.substr(start, count);
if(!hasDuplication(substring, position))
{
if(count > longest)
longest = count;
}
else
break;
}
}
delete[] position;
return longest;
}
bool hasDuplication(const std::string& str, int position[])
{
for(int i = 0; i < 26; ++i)
position[i] = -1;
for(int i = 0; i < str.length(); ++i)
{
int indexInPosition = str[i] - 'a';
if(position[indexInPosition] >= 0)
return true;
position[indexInPosition] = indexInPosition;
}
return false;
}
// 方法一:动态规划
int longestSubstringWithoutDuplication_2(const std::string& str)
{
int curLength = 0;
int maxLength = 0;
int* position = new int[26];
for(int i = 0; i < 26; ++i)
position[i] = -1;
for(int i = 0; i < str.length(); ++i)
{
int prevIndex = position[str[i] - 'a'];
if(prevIndex < 0 || i - prevIndex > curLength)
++curLength;
else
{
if(curLength > maxLength)
maxLength = curLength;
curLength = i - prevIndex;
}
position[str[i] - 'a'] = i;
}
if(curLength > maxLength)
maxLength = curLength;
delete[] position;
return maxLength;
}
我们创建了一个长度为26的数组来储存每个字符上次出现在字符串中位置的下标。我们在扫描字符串时遇到某个字符,就把该字符在字符串中的位置储存到数组对应的元素中。
丑数
题目:我们把只包含因子2、3和5的数称作丑数(Ugly Number)。求按从小到大的顺序的第1500个丑数。例如6、8都是丑数,但14不是,因为它包含因子7。习惯上我们把1当做第一个丑数。
思路:创建数组保存已经找到的丑数,用空间换时间的解法
我们可以创建一个数组,里面的数字是排序好的丑数,每个丑数都是前面的丑数乘以2、3、5得到的。对于乘以2而言,肯定存在某一丑数T2,排在它之前的每个丑数乘以2得到的结果都会小于已有最大的丑数,排在它之前的每个丑数乘以2得到的结果都会太大。我们只需记下这个丑数的位置,同时每次生成新的丑数时去更新这个T2即可。对于3、5而言,也存在同样的T3和5。
// ====================算法1的代码====================
bool IsUgly(int number)
{
while(number % 2 == 0)
number /= 2;
while(number % 3 == 0)
number /= 3;
while(number % 5 == 0)
number /= 5;
return (number == 1) ? true : false;
}
int GetUglyNumber_Solution1(int index)
{
if(index <= 0)
return 0;
int number = 0;
int uglyFound = 0;
while(uglyFound < index)
{
++number;
if(IsUgly(number))
++uglyFound;
}
return number;
}
// ====================算法2的代码====================
int Min(int number1, int number2, int number3);
int GetUglyNumber_Solution2(int index)
{
if(index <= 0)
return 0;
int *pUglyNumbers = new int[index];
pUglyNumbers[0] = 1;
int nextUglyIndex = 1;
int *pMultiply2 = pUglyNumbers;
int *pMultiply3 = pUglyNumbers;
int *pMultiply5 = pUglyNumbers;
while(nextUglyIndex < index)
{
int min = Min(*pMultiply2 * 2, *pMultiply3 * 3, *pMultiply5 * 5);
pUglyNumbers[nextUglyIndex] = min;
while(*pMultiply2 * 2 <= pUglyNumbers[nextUglyIndex])
++pMultiply2;
while(*pMultiply3 * 3 <= pUglyNumbers[nextUglyIndex])
++pMultiply3;
while(*pMultiply5 * 5 <= pUglyNumbers[nextUglyIndex])
++pMultiply5;
++nextUglyIndex;
}
int ugly = pUglyNumbers[nextUglyIndex - 1];
delete[] pUglyNumbers;
return ugly;
}
int Min(int number1, int number2, int number3)
{
int min = (number1 < number2) ? number1 : number2;
min = (min < number3) ? min : number3;
return min;
}
字符串中第一个只出现一次的字符
题目:在字符串中找出第一个只出现一次的字符。如输入”abaccdeff”,则输出’b’。
思路:使用哈希表来存放每个字符的出现次数。字符(char)是一个长度为8的数据类型,因此总共又怒256种可能。于是我们创建一个长度为256的数组,每个字母根据其ASCII码值作为数组的下标对于数组的一个数字,而数组中储存的是每个字符出现的次数。这样我们就创建来一个大小为256、以字符ASCII码为键值的哈希表。
char FirstNotRepeatingChar(const char* pString)
{
if(pString == nullptr)
return '\0';
const int tableSize = 256;
unsigned int hashTable[tableSize];
for(unsigned int i = 0; i < tableSize; ++i)
hashTable[i] = 0;
const char* pHashKey = pString;
while(*(pHashKey) != '\0')
hashTable[*(pHashKey++)] ++;
pHashKey = pString;
while(*pHashKey != '\0')
{
if(hashTable[*pHashKey] == 1)
return *pHashKey;
pHashKey++;
}
return '\0';
}
本题拓展:在前面的例子中,我们之所以可以把哈希表的大小设为256,是因为字符(char)是8bit的类型,总共只有256个字符。但实际上字符不只是256个,比如中文就有几千个汉字。如果题目要求考虑汉子,那么前面的算法是不是有问题?怎么解决?

举一反三:如果需要判断多个字符是不是在某个字符里面出现过或者统计多个字符在某个字符串中出现的次数,那么我们可以考虑基于数组创建一个简单的哈希表,这样可以用很小的空间消耗换来时间效率的提升。
字符流中第一个只出现一次的字符
题目:请实现一个函数用来找出字符流中第一个只出现一次的字符。例如,当从字符流中只读出前两个字符”go”时,第一个只出现一次的字符是’g’。当从该字符流中读出前六个字符”google”时,第一个只出现一次的字符是’l’。
思路:哈希表用数组实现,数组中的元素occurrence[i]和ASCII码的值为i的字符相对应。最开始时,都初始化为-1,当第一次从字符流中读出时,更新为它在字符流中的位置。当再次读出时,更新为-2。
class CharStatistics
{
public:
CharStatistics() : index(0)
{
for(int i = 0; i < 256; ++i)
occurrence[i] = -1;
}
void Insert(char ch)
{
if(occurrence[ch] == -1)
occurrence[ch] = index;
else if(occurrence[ch] >= 0)
occurrence[ch] = -2;
index++;
}
char FirstAppearingOnce()
{
char ch = '\0';
int minIndex = numeric_limits<int>::max();
for(int i = 0; i < 256; ++i)
{
if(occurrence[i] >= 0 && occurrence[i] < minIndex)
{
ch = (char) i;
minIndex = occurrence[i];
}
}
return ch;
}
private:
// occurrence[i]: A character with ASCII value i;
// occurrence[i] = -1: The character has not found;
// occurrence[i] = -2: The character has been found for mutlple times
// occurrence[i] >= 0: The character has been found only once
int occurrence[256];
int index;
};
数组中的逆序对
题目:在数组中的两个数字如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
思路:先把数组分割成子数组,统计出子数组内部的逆序对的数目,然后再统计出两个相邻子数组之间的逆序对的数目。在统计逆序对的过程中,还需要对数组进行排序。我们不难发现这个排序对过程实际上就是归并排序。
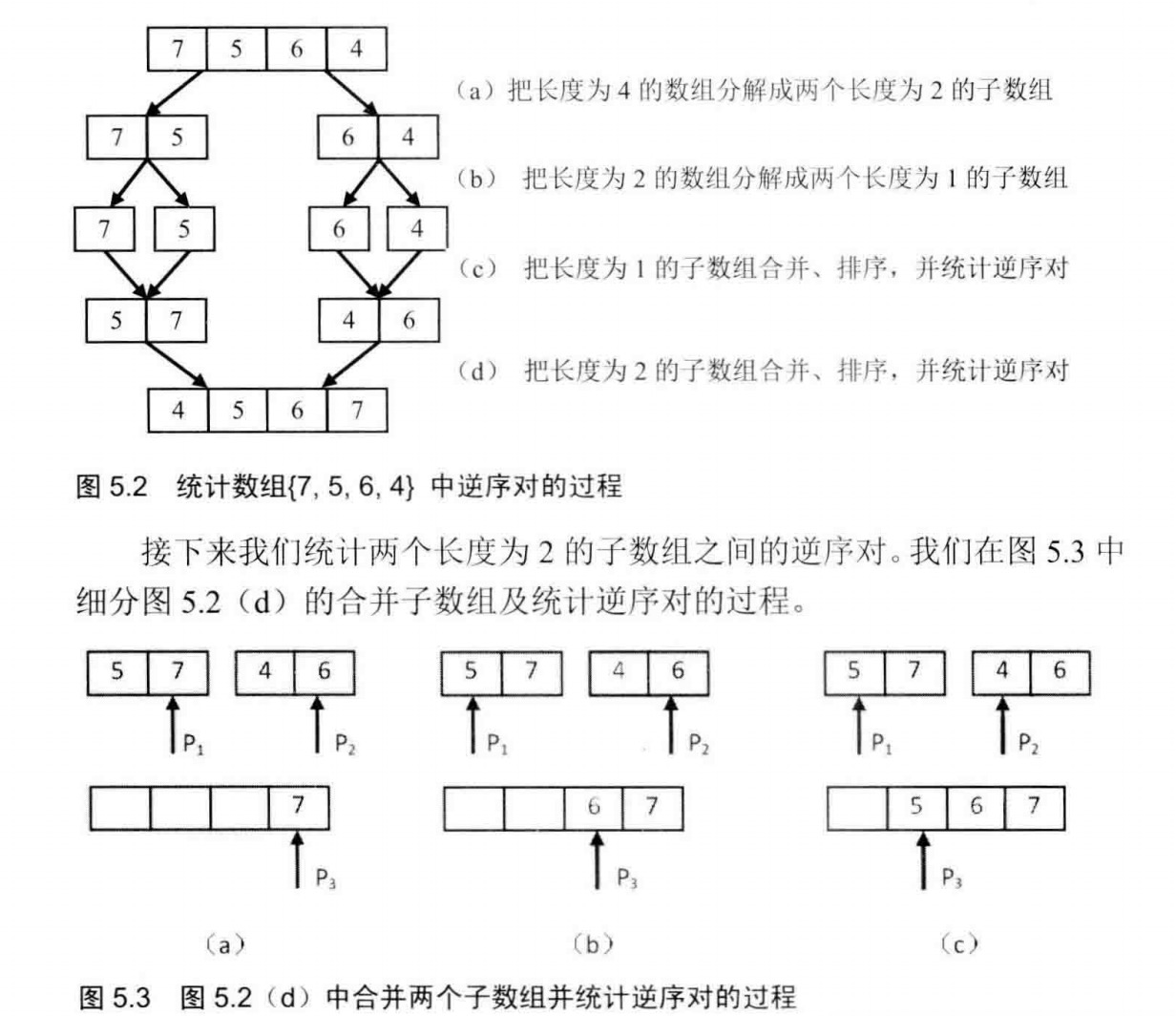
int InversePairsCore(int* data, int* copy, int start, int end);
int InversePairs(int* data, int length)
{
if(data == nullptr || length < 0)
return 0;
int* copy = new int[length];
for(int i = 0; i < length; ++i)
copy[i] = data[i];
int count = InversePairsCore(data, copy, 0, length - 1);
delete[] copy;
return count;
}
int InversePairsCore(int* data, int* copy, int start, int end)
{
if(start == end)
{
copy[start] = data[start];
return 0;
}
int length = (end - start) / 2;
int left = InversePairsCore(copy, data, start, start + length);
int right = InversePairsCore(copy, data, start + length + 1, end);
// i初始化为前半段最后一个数字的下标
int i = start + length;
// j初始化为后半段最后一个数字的下标
int j = end;
int indexCopy = end;
int count = 0;
while(i >= start && j >= start + length + 1)
{
if(data[i] > data[j])
{
copy[indexCopy--] = data[i--];
count += j - start - length;
}
else
{
copy[indexCopy--] = data[j--];
}
}
for(; i >= start; --i)
copy[indexCopy--] = data[i];
for(; j >= start + length + 1; --j)
copy[indexCopy--] = data[j];
return left + right + count;
}
两个链表的第一个公共结点
题目:输入两个链表,找出它们的第一个公共结点。
思路:首先遍历两个链表得到它们的长度,就能知道长的链表比短的链表多几个节点。在第二次遍历时,在较长的链表上先走若干步,接着同时在两个链表上遍历,找到的第一个相同的节点就是它们的第一个公共节点。
unsigned int GetListLength(ListNode* pHead);
ListNode* FindFirstCommonNode(ListNode *pHead1, ListNode *pHead2)
{
// 得到两个链表的长度
unsigned int nLength1 = GetListLength(pHead1);
unsigned int nLength2 = GetListLength(pHead2);
int nLengthDif = nLength1 - nLength2;
ListNode* pListHeadLong = pHead1;
ListNode* pListHeadShort = pHead2;
if(nLength2 > nLength1)
{
pListHeadLong = pHead2;
pListHeadShort = pHead1;
nLengthDif = nLength2 - nLength1;
}
// 先在长链表上走几步,再同时在两个链表上遍历
for(int i = 0; i < nLengthDif; ++i)
pListHeadLong = pListHeadLong->m_pNext;
while((pListHeadLong != nullptr) &&
(pListHeadShort != nullptr) &&
(pListHeadLong != pListHeadShort))
{
pListHeadLong = pListHeadLong->m_pNext;
pListHeadShort = pListHeadShort->m_pNext;
}
// 得到第一个公共结点
ListNode* pFisrtCommonNode = pListHeadLong;
return pFisrtCommonNode;
}
unsigned int GetListLength(ListNode* pHead)
{
unsigned int nLength = 0;
ListNode* pNode = pHead;
while(pNode != nullptr)
{
++nLength;
pNode = pNode->m_pNext;
}
return nLength;
}
数字在排序数组中出现的次数
题目:统计一个数字在排序数组中出现的次数。例如输入排序数组{1, 2, 3, 3, 3, 3, 4, 5}和数字3,由于3在这个数组中出现了4次,因此输出4。
思路:使用二分查找算法在数组中找到第一个k和最后一个k。
int GetFirstK(const int* data, int length, int k, int start, int end);
int GetLastK(const int* data, int length, int k, int start, int end);
int GetNumberOfK(const int* data, int length, int k)
{
int number = 0;
if(data != nullptr && length > 0)
{
int first = GetFirstK(data, length, k, 0, length - 1);
int last = GetLastK(data, length, k, 0, length - 1);
if(first > -1 && last > -1)
number = last - first + 1;
}
return number;
}
// 找到数组中第一个k的下标。如果数组中不存在k,返回-1
int GetFirstK(const int* data, int length, int k, int start, int end)
{
if(start > end)
return -1;
int middleIndex = (start + end) / 2;
int middleData = data[middleIndex];
if(middleData == k)
{
if((middleIndex > 0 && data[middleIndex - 1] != k)
|| middleIndex == 0)
return middleIndex;
else
end = middleIndex - 1;
}
else if(middleData > k)
end = middleIndex - 1;
else
start = middleIndex + 1;
return GetFirstK(data, length, k, start, end);
}
// 找到数组中最后一个k的下标。如果数组中不存在k,返回-1
int GetLastK(const int* data, int length, int k, int start, int end)
{
if(start > end)
return -1;
int middleIndex = (start + end) / 2;
int middleData = data[middleIndex];
if(middleData == k)
{
if((middleIndex < length - 1 && data[middleIndex + 1] != k)
|| middleIndex == length - 1)
return middleIndex;
else
start = middleIndex + 1;
}
else if(middleData < k)
start = middleIndex + 1;
else
end = middleIndex - 1;
return GetLastK(data, length, k, start, end);
}
0到n-1中缺失的数字
题目:一个长度为n-1的递增排序数组中的所有数字都是唯一的,并且每个数字都在范围0到n-1之内。在范围0到n-1的n个数字中有且只有一个数字不在该数组中,请找出这个数字。
思路:因为是递增数组,如果不在数组中的那个数字记为m,那么所有比m小的数字的下标与它们的值相同,而比m大的数字的下标与它们的值不同。所有问题转换成在排序数组中找出第一个值和下标不相等的元素。我们可以基于二分查找来找到它。
int GetMissingNumber(const int* numbers, int length)
{
if(numbers == nullptr || length <= 0)
return -1;
int left = 0;
int right = length - 1;
while(left <= right)
{
int middle = (right + left) >> 1;
if(numbers[middle] != middle)
{
if(middle == 0 || numbers[middle - 1] == middle - 1)
return middle;
right = middle - 1;
}
else
left = middle + 1;
}
if(left == length)
return length;
// 无效的输入,比如数组不是按要求排序的,
// 或者有数字不在0到n-1范围之内
return -1;
}
数组中数值和下标相等的元素
题目:假设一个单调递增的数组里的每个元素都是整数并且是唯一的。请编程实现一个函数找出数组中任意一个数值等于其下标的元素。例如,在数组{-3, -1,1, 3, 5}中,数字3和它的下标相等。
思路:二分查找,由于数组中的所有数字唯一并且单调递增,如果第i个数字的值大于i,那么它右边的数字都大于对应的下标;如果第i个数字的值小于i,那么它左边的数字都小于对应的下标。
int GetNumberSameAsIndex(const int* numbers, int length)
{
if(numbers == nullptr || length <= 0)
return -1;
int left = 0;
int right = length - 1;
while(left <= right)
{
int middle = left + ((right - left) >> 1);
if(numbers[middle] == middle)
return middle;
if(numbers[middle] > middle)
right = middle - 1;
else
left = middle + 1;
}
return -1;
}
二叉搜索树的第k个结点
题目:给定一棵二叉搜索树,请找出其中的第k大的结点。
思路:如果按照中序遍历的顺序遍历一颗二叉搜索树,则遍历序列的数值是递增排序的。因此我们可以很容易找出它的第k大节点。
const BinaryTreeNode* KthNodeCore(const BinaryTreeNode* pRoot, unsigned int& k);
const BinaryTreeNode* KthNode(const BinaryTreeNode* pRoot, unsigned int k)
{
if(pRoot == nullptr || k == 0)
return nullptr;
return KthNodeCore(pRoot, k);
}
const BinaryTreeNode* KthNodeCore(const BinaryTreeNode* pRoot, unsigned int& k)
{
const BinaryTreeNode* target = nullptr;
if(pRoot->m_pLeft != nullptr)
target = KthNodeCore(pRoot->m_pLeft, k);
if(target == nullptr)
{
if(k == 1)
target = pRoot;
k--;
}
if(target == nullptr && pRoot->m_pRight != nullptr)
target = KthNodeCore(pRoot->m_pRight, k);
return target;
}
二叉树的深度
题目:输入一棵二叉树的根结点,求该树的深度。从根结点到叶结点依次经过的结点(含根、叶结点)形成树的一条路径,最长路径的长度为树的深度。
int TreeDepth(const BinaryTreeNode* pRoot)
{
if(pRoot == nullptr)
return 0;
int nLeft = TreeDepth(pRoot->m_pLeft);
int nRight = TreeDepth(pRoot->m_pRight);
return (nLeft > nRight) ? (nLeft + 1) : (nRight + 1);
}
平衡二叉树
题目:输入一棵二叉树的根结点,判断该树是不是平衡二叉树。如果某二叉树中任意结点的左右子树的深度相差不超过1,那么它就是一棵平衡二叉树。
方法一:遍历树的每个节点的时候,调用函数TreeDepth得到它的左、右子树的深度。如果相差不超过1,那么他就是一颗平衡二叉树。但这里一个节点会被重复遍历多次,时间效率不高。
方法二:使用后序遍历但方式遍历二叉树的每个节点,那么在遍历到一个节点之前我们就已经遍历了它的左、右子树。只要在遍历每个节点的时候记录它的深度,我们就可以一边遍历一边判断每个节点是不是平衡的。
// ====================方法1====================
int TreeDepth(const BinaryTreeNode* pRoot)
{
if(pRoot == nullptr)
return 0;
int nLeft = TreeDepth(pRoot->m_pLeft);
int nRight = TreeDepth(pRoot->m_pRight);
return (nLeft > nRight) ? (nLeft + 1) : (nRight + 1);
}
bool IsBalanced_Solution1(const BinaryTreeNode* pRoot)
{
if(pRoot == nullptr)
return true;
int left = TreeDepth(pRoot->m_pLeft);
int right = TreeDepth(pRoot->m_pRight);
int diff = left - right;
if(diff > 1 || diff < -1)
return false;
return IsBalanced_Solution1(pRoot->m_pLeft)
&& IsBalanced_Solution1(pRoot->m_pRight);
}
// ====================方法2====================
bool IsBalanced(const BinaryTreeNode* pRoot, int* pDepth);
bool IsBalanced_Solution2(const BinaryTreeNode* pRoot)
{
int depth = 0;
return IsBalanced(pRoot, &depth);
}
bool IsBalanced(const BinaryTreeNode* pRoot, int* pDepth)
{
if(pRoot == nullptr)
{
*pDepth = 0;
return true;
}
int left, right;
if(IsBalanced(pRoot->m_pLeft, &left)
&& IsBalanced(pRoot->m_pRight, &right))
{
int diff = left - right;
if(diff <= 1 && diff >= -1)
{
*pDepth = 1 + (left > right ? left : right);
return true;
}
}
return false;
}
数组中只出现一次的两个数字
题目:一个整型数组里除了两个数字之外,其他的数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是O(n),空间复杂度是O(1)。
思路:任何一个数字异或它自己都等于0。也就是说,如果我们从头到尾依次异或数组中的每个数字,那么最终的结果刚好是那两个只出现一次的数字的异或结果,因为那些成对出现的数字全部在异或中抵消了。
由于两个数字肯定不一样,那么异或的结果肯定不为0,也就是说,在这个结果数字的二进制表示中至少有一位为1。我们在结果数字中找到第一个为1的位的位置,记为第n位。现在我们以第n位是不是1为标准把原数组中的数字分为两个数组,那么出现了两次的数字肯定被分到同一数组。因为两个相同的数字的任意一位都是相同的,我们不可能把相同的数字分到两个字数组中去,于是我们已经把原数组分成了两个数组,每个数组都包含一个只出现一次的数字,而其他数字都出现了两次。
unsigned int FindFirstBitIs1(int num);
bool IsBit1(int num, unsigned int indexBit);
void FindNumsAppearOnce(int data[], int length, int* num1, int* num2)
{
if(data == nullptr || length < 2)
return;
int resultExclusiveOR = 0;
for(int i = 0; i < length; ++i)
resultExclusiveOR ^= data[i];
unsigned int indexOf1 = FindFirstBitIs1(resultExclusiveOR);
*num1 = *num2 = 0;
for(int j = 0; j < length; ++j)
{
if(IsBit1(data[j], indexOf1))
*num1 ^= data[j];
else
*num2 ^= data[j];
}
}
// 找到num从右边数起第一个是1的位
unsigned int FindFirstBitIs1(int num)
{
int indexBit = 0;
while(((num & 1) == 0) && (indexBit < 8 * sizeof(int)))
{
num = num >> 1;
++indexBit;
}
return indexBit;
}
// 判断数字num的第indexBit位是不是1
bool IsBit1(int num, unsigned int indexBit)
{
num = num >> indexBit;
return (num & 1);
}
数组中唯一只出现一次的数字
题目:在一个数组中除了一个数字只出现一次之外,其他数字都出现了三次。请找出那个吃出现一次的数字。
思路:如果一个数字出现三次,那么它的二进制表示的每一位(0或者1)也出现三次。如果把所有出现三次的数字的二进制表示的每一位分别加起来,那么每一位的和都能被3整除。
我们把数组中所有数字的二进制表示的每一位都加起来。如果某一位的和能被3整除,那么那个只出现一次的数字二进制表示中对应的那一位是0;否则就是1。
int FindNumberAppearingOnce(int numbers[], int length)
{
if(numbers == nullptr || length <= 0)
throw new std::exception("Invalid input.");
int bitSum[32] = {0};
for(int i = 0; i < length; ++i)
{
int bitMask = 1;
for(int j = 31; j >= 0; --j)
{
int bit = numbers[i] & bitMask;
if(bit != 0)
bitSum[j] += 1;
bitMask = bitMask << 1;
}
}
int result = 0;
for(int i = 0; i < 32; ++i)
{
result = result << 1;
result += bitSum[i] % 3;
}
return result;
}
这种解决时间复杂度是O(n)。我们需要一个长度位32的辅助数组储存二进制表示的每一位的和。由于数组长度是固定的,因此空间复杂度是O(1)。我们也可以很容易从排序的数组中找到只出现一次的数字,但排序需要O(nlogn)时间。
和为s的两个数字
题目:输入一个递增排序的数组和一个数字s,在数组中查找两个数,使得它们的和正好是s。如果有多对数字的和等于s,输出任意一对即可。
思路:因为是递增排序的数组,我使用两个指针,一个指向第一个数字,一个指向最后一个数字,然后往中间遍历直到找到和为s的两个数。时间复杂度是O(n)。
bool FindNumbersWithSum(int data[], int length, int sum,
int* num1, int* num2)
{
bool found = false;
if(length < 1 || num1 == nullptr || num2 == nullptr)
return found;
int ahead = length - 1;
int behind = 0;
while(ahead > behind)
{
long long curSum = data[ahead] + data[behind];
if(curSum == sum)
{
*num1 = data[behind];
*num2 = data[ahead];
found = true;
break;
}
else if(curSum > sum)
ahead --;
else
behind ++;
}
return found;
}
和为s的连续正数序列
题目:输入一个正数s,打印出所有和为s的连续正数序列(至少含有两个数)。例如输入15,由于1+2+3+4+5=4+5+6=7+8=15,所以结果打印出3个连续序列1~5、4~6和7~8。
思路:我们定义两个指针small、big,分别初始化为1、2。如果从small到big的序列的和大于s,则可以从序列中去掉较小的值,也就是增大small的值。如果从small到big的序列的和小于s,则可以增大big,让这个序列包含更多的数字。因为这个序列至少需要两个数字,我们一直增加small到(1+s)/2为止。
void PrintContinuousSequence(int small, int big);
void FindContinuousSequence(int sum)
{
if(sum < 3)
return;
int small = 1;
int big = 2;
int middle = (1 + sum) / 2;
int curSum = small + big;
while(small < middle)
{
if(curSum == sum)
PrintContinuousSequence(small, big);
while(curSum > sum && small < middle)
{
curSum -= small;
small ++;
if(curSum == sum)
PrintContinuousSequence(small, big);
}
big ++;
curSum += big;
}
}
void PrintContinuousSequence(int small, int big)
{
for(int i = small; i <= big; ++ i)
printf("%d ", i);
printf("\n");
}
翻转单词顺序
题目:输入一个英文句子,翻转句子中单词的顺序,但单词内字符的顺序不变。为简单起见,标点符号和普通字母一样处理。例如输入字符串”I am a student. “,则输出”student. a am I”。
思路:先翻转句子中的所有字符,在翻转每个单词。
void Reverse(char *pBegin, char *pEnd)
{
if(pBegin == nullptr || pEnd == nullptr)
return;
while(pBegin < pEnd)
{
char temp = *pBegin;
*pBegin = *pEnd;
*pEnd = temp;
pBegin ++, pEnd --;
}
}
char* ReverseSentence(char *pData)
{
if(pData == nullptr)
return nullptr;
char *pBegin = pData;
char *pEnd = pData;
while(*pEnd != '\0')
pEnd ++;
pEnd--;
// 翻转整个句子
Reverse(pBegin, pEnd);
// 翻转句子中的每个单词
pBegin = pEnd = pData;
while(*pBegin != '\0')
{
if(*pBegin == ' ')
{
pBegin ++;
pEnd ++;
}
else if(*pEnd == ' ' || *pEnd == '\0')
{
Reverse(pBegin, --pEnd);
pBegin = ++pEnd;
}
else
pEnd ++;
}
return pData;
}
左旋转字符串
题目:字符串的左旋转操作是把字符串前面的若干个字符转移到字符串的尾部。请定义一个函数实现字符串左旋转操作的功能。比如输入字符串”abcdefg”和数字2,该函数将返回左旋转2位得到的结果”cdefgab”。
思路:通关翻转字符的办法可以解决这个问题。
char* LeftRotateString(char* pStr, int n)
{
if(pStr != nullptr)
{
int nLength = static_cast<int>(strlen(pStr));
if(nLength > 0 && n > 0 && n < nLength)
{
char* pFirstStart = pStr;
char* pFirstEnd = pStr + n - 1;
char* pSecondStart = pStr + n;
char* pSecondEnd = pStr + nLength - 1;
// 翻转字符串的前面n个字符
Reverse(pFirstStart, pFirstEnd);
// 翻转字符串的后面部分
Reverse(pSecondStart, pSecondEnd);
// 翻转整个字符串
Reverse(pFirstStart, pSecondEnd);
}
}
return pStr;
}
滑动窗口的最大值
题目:给定一个数组和滑动窗口的大小,请找出所有滑动窗口里的最大值。例如,如果输入数组{2, 3, 4, 2, 6, 2, 5, 1}及滑动窗口的大小3,那么一共存在6个滑动窗口,它们的最大值分别为{4, 4, 6, 6, 6, 5}。
思路:我们把有可能成为滑动窗口最大值的数值存入一个两端开口的队列。
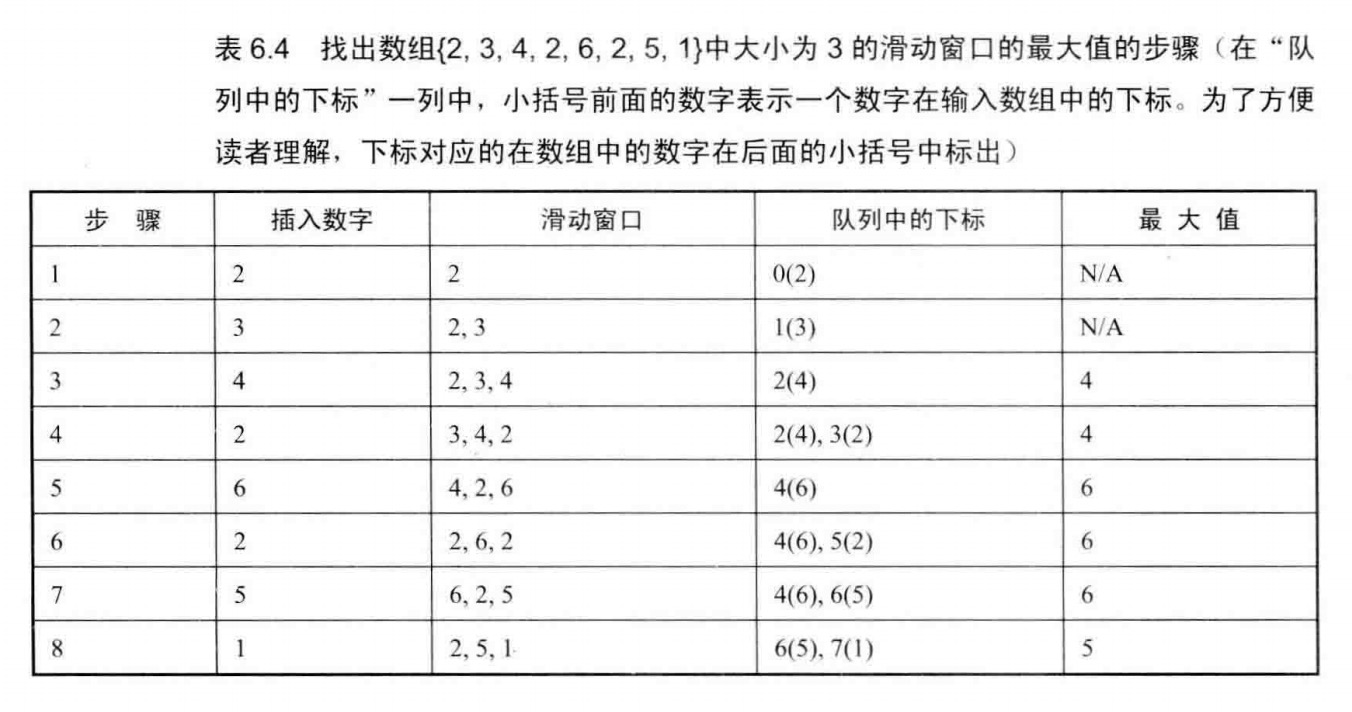
这里在队列里存入数字在数组的下标,而不是数值。当一个数字的下标与当前处理的数字的下标之差大于或者等于滑动窗口的大小时,这个数字已经从窗口中滑出,可以从队列中删除了。
vector<int> maxInWindows(const vector<int>& num, unsigned int size)
{
vector<int> maxInWindows;
if(num.size() >= size && size >= 1)
{
deque<int> index;
for(unsigned int i = 0; i < size; ++i)
{
while(!index.empty() && num[i] >= num[index.back()])
index.pop_back();
index.push_back(i);
}
for(unsigned int i = size; i < num.size(); ++i)
{
maxInWindows.push_back(num[index.front()]);
while(!index.empty() && num[i] >= num[index.back()])
index.pop_back();
if(!index.empty() && index.front() <= (int) (i - size))
index.pop_front();
index.push_back(i);
}
maxInWindows.push_back(num[index.front()]);
}
return maxInWindows;
}
队列的最大值
题目:请定义一个队列并实现函数max得到队列里面的最大值,要求函数max、push_back和pop_front的时间复杂度都是O(1)。
思路:滑动窗口可以看成一个队列,因此上题的解法可以用来实现带max函数的队列。
template<typename T> class QueueWithMax
{
public:
QueueWithMax() : currentIndex(0)
{
}
void push_back(T number)
{
while(!maximums.empty() && number >= maximums.back().number)
maximums.pop_back();
InternalData internalData = { number, currentIndex };
data.push_back(internalData);
maximums.push_back(internalData);
++currentIndex;
}
void pop_front()
{
if(maximums.empty())
throw new exception("queue is empty");
if(maximums.front().index == data.front().index)
maximums.pop_front();
data.pop_front();
}
T max() const
{
if(maximums.empty())
throw new exception("queue is empty");
return maximums.front().number;
}
private:
struct InternalData
{
T number;
int index;
};
deque<InternalData> data;
deque<InternalData> maximums;
int currentIndex;
};
n个骰子的点数
题目:把n个骰子扔在地上,所有骰子朝上一面的点数之和为s。输入n,打印出s的所有可能的值出现的概率。
解法一:基于递归求骰子点数,时间效率不够高。定义一个长度为6n-n+1的数组,将和为s的点数出现的次数保存到数组的第s-n个元素里。
解法二:基于循环求骰子点数,时间性能好。我们可以考虑用两个数组来储存骰子点数的每个总数出现的次数。在一轮循环中,第一个数组中的第n个数字表示骰子和为n出现的次数。在下一轮循环中,我们加上一个新的骰子,此时和为n的骰子出现的次数应该等于上一轮循环中骰子点数和为n-1、n-2、n-3、n-4、n-5与n-6的次数的总和。
int g_maxValue = 6;
// ====================方法一====================
void Probability(int number, int* pProbabilities);
void Probability(int original, int current, int sum, int* pProbabilities);
void PrintProbability_Solution1(int number)
{
if(number < 1)
return;
int maxSum = number * g_maxValue;
int* pProbabilities = new int[maxSum - number + 1];
for(int i = number; i <= maxSum; ++i)
pProbabilities[i - number] = 0;
Probability(number, pProbabilities);
int total = pow((double)g_maxValue, number);
for(int i = number; i <= maxSum; ++i)
{
double ratio = (double)pProbabilities[i - number] / total;
printf("%d: %e\n", i, ratio);
}
delete[] pProbabilities;
}
void Probability(int number, int* pProbabilities)
{
for(int i = 1; i <= g_maxValue; ++i)
Probability(number, number, i, pProbabilities);
}
void Probability(int original, int current, int sum,
int* pProbabilities)
{
if(current == 1)
{
pProbabilities[sum - original]++;
}
else
{
for(int i = 1; i <= g_maxValue; ++i)
{
Probability(original, current - 1, i + sum, pProbabilities);
}
}
}
// ====================方法二====================
void PrintProbability_Solution2(int number)
{
if(number < 1)
return;
int* pProbabilities[2];
pProbabilities[0] = new int[g_maxValue * number + 1];
pProbabilities[1] = new int[g_maxValue * number + 1];
for(int i = 0; i < g_maxValue * number + 1; ++i)
{
pProbabilities[0][i] = 0;
pProbabilities[1][i] = 0;
}
int flag = 0;
for (int i = 1; i <= g_maxValue; ++i)
pProbabilities[flag][i] = 1;
for (int k = 2; k <= number; ++k)
{
for(int i = 0; i < k; ++i)
pProbabilities[1 - flag][i] = 0;
for (int i = k; i <= g_maxValue * k; ++i)
{
pProbabilities[1 - flag][i] = 0;
for(int j = 1; j <= i && j <= g_maxValue; ++j)
pProbabilities[1 - flag][i] += pProbabilities[flag][i - j];
}
flag = 1 - flag;
}
double total = pow((double)g_maxValue, number);
for(int i = number; i <= g_maxValue * number; ++i)
{
double ratio = (double)pProbabilities[flag][i] / total;
printf("%d: %e\n", i, ratio);
}
delete[] pProbabilities[0];
delete[] pProbabilities[1];
}
扑克牌的顺子
题目:从扑克牌中随机抽5张牌,判断是不是一个顺子,即这5张牌是不是连续的。2~10为数字本身,A为1,J为11,Q为12,K为13,而大、小王可以看成任意数字。
思路:我们把大、小王定义为0,这样就能和其他扑克牌区分开来了。我们要做3件事:首先把数组排序;其次统计数组中0的个数;最后统计排序之后的数组中相邻数字之间的空缺总数。如果空缺总数小于或者等于0的个数,那么这个数组就是连续的;反之则不连续。
int Compare(const void *arg1, const void *arg2);
bool IsContinuous(int* numbers, int length)
{
if(numbers == nullptr || length < 1)
return false;
qsort(numbers, length, sizeof(int), Compare);
int numberOfZero = 0;
int numberOfGap = 0;
// 统计数组中0的个数
for(int i = 0; i < length && numbers[i] == 0; ++i)
++numberOfZero;
// 统计数组中的间隔数目
int small = numberOfZero;
int big = small + 1;
while(big < length)
{
// 两个数相等,有对子,不可能是顺子
if(numbers[small] == numbers[big])
return false;
numberOfGap += numbers[big] - numbers[small] - 1;
small = big;
++big;
}
return (numberOfGap > numberOfZero) ? false : true;
}
int Compare(const void *arg1, const void *arg2)
{
return *(int*) arg1 - *(int*) arg2;
}
圆圈中最后剩下的数字
题目:0, 1, …, n-1这n个数字排成一个圆圈,从数字0开始每次从这个圆圈里删除第m个数字。求出这个圆圈里剩下的最后一个数字。
解法一:用环形链表模拟圆圈
解法二:

// ====================方法1====================
int LastRemaining_Solution1(unsigned int n, unsigned int m)
{
if(n < 1 || m < 1)
return -1;
unsigned int i = 0;
list<int> numbers;
for(i = 0; i < n; ++ i)
numbers.push_back(i);
list<int>::iterator current = numbers.begin();
while(numbers.size() > 1)
{
for(int i = 1; i < m; ++ i)
{
current ++;
if(current == numbers.end())
current = numbers.begin();
}
list<int>::iterator next = ++ current;
if(next == numbers.end())
next = numbers.begin();
-- current;
numbers.erase(current);
current = next;
}
return *(current);
}
// ====================方法2====================
int LastRemaining_Solution2(unsigned int n, unsigned int m)
{
if(n < 1 || m < 1)
return -1;
int last = 0;
for (int i = 2; i <= n; i ++)
last = (last + m) % i;
return last;
}
股票的最大利润
题目:假设把某股票的价格按照时间先后顺序存储在数组中,请问买卖交易该股票可能获得的利润是多少?例如一只股票在某些时间节点的价格为{9, 11, 8, 5,7, 12, 16, 14}。如果我们能在价格为5的时候买入并在价格为16时卖出,则能收获最大的利润11。
思路:我们先定义函数diff(i)为当卖出价为数组中第i个数字时可能获得的最大利润。显然,再卖出价固定时,买入价越低获得的利润越大。也就是说,如果在扫描到数组中的第i个数字时,只要我们能够记住之前的i-i个数字中的最小值,就能算出在当前价位卖出时可能得到的最大利润。
int MaxDiff(const int* numbers, unsigned length)
{
if(numbers == nullptr && length < 2)
return 0;
int min = numbers[0];
int maxDiff = numbers[1] - min;
for(int i = 2; i < length; ++i)
{
if(numbers[i - 1] < min)
min = numbers[i - 1];
int currentDiff = numbers[i] - min;
if(currentDiff > maxDiff)
maxDiff = currentDiff;
}
return maxDiff;
}
求1+2+…+n
题目:求1+2+…+n,要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句(A?B:C)。
// ====================方法一====================
class Temp
{
public:
Temp() { ++ N; Sum += N; }
static void Reset() { N = 0; Sum = 0; }
static unsigned int GetSum() { return Sum; }
private:
static unsigned int N;
static unsigned int Sum;
};
unsigned int Temp::N = 0;
unsigned int Temp::Sum = 0;
unsigned int Sum_Solution1(unsigned int n)
{
Temp::Reset();
Temp *a = new Temp[n];
delete []a;
a = NULL;
return Temp::GetSum();
}
// ====================方法二====================
class A;
A* Array[2];
class A
{
public:
virtual unsigned int Sum (unsigned int n)
{
return 0;
}
};
class B: public A
{
public:
virtual unsigned int Sum (unsigned int n)
{
return Array[!!n]->Sum(n-1) + n;
}
};
int Sum_Solution2(int n)
{
A a;
B b;
Array[0] = &a;
Array[1] = &b;
int value = Array[1]->Sum(n);
return value;
}
// ====================方法三====================
typedef unsigned int (*fun)(unsigned int);
unsigned int Solution3_Teminator(unsigned int n)
{
return 0;
}
unsigned int Sum_Solution3(unsigned int n)
{
static fun f[2] = {Solution3_Teminator, Sum_Solution3};
return n + f[!!n](n - 1);
}
// ====================方法四====================
template <unsigned int n> struct Sum_Solution4
{
enum Value { N = Sum_Solution4<n - 1>::N + n};
};
template <> struct Sum_Solution4<1>
{
enum Value { N = 1};
};
template <> struct Sum_Solution4<0>
{
enum Value { N = 0};
};
不用加减乘除做加法
题目:写一个函数,求两个整数之和,要求在函数体内不得使用+、-、×、÷四则运算符号。
思路:第一步不考虑进位对每一位相加。0加0、1加1的结果都是0,0加1、1加1的结果都是1。我们注意到,这和异或的结果是一样的。接着考虑第二步进位,对0加0、0加1、1加0而言,都不会产生进位,只有1加1时,会向前产生一个进位。此时我们可以想象成两个数先做位与运算,然后再想左移动一位。第三步把前两个步骤的结果相加。第三步相加的过程依然是重复前面的两步,直到不产生进位为止。
#include <cstdio>
int Add(int num1, int num2)
{
int sum, carry;
do
{
sum = num1 ^ num2;
carry = (num1 & num2) << 1;
num1 = sum;
num2 = carry;
}
while(num2 != 0);
return num1;
}
相关问题:不使用新的变量,交换两个变量的值。比如有两个变量a、b,我们希望交换它们的值。有两种不同的方法:

构建乘积数组
题目:给定一个数组A[0, 1, …, n-1],请构建一个数组B[0, 1, …, n-1],其中B中的元素B[i] =A[0]×A[1]×… ×A[i-1]×A[i+1]×…×A[n-1]。不能使用除法。

void BuildProductionArray(const vector<double>& input, vector<double>& output)
{
int length1 = input.size();
int length2 = output.size();
if(length1 == length2 && length2 > 1)
{
output[0] = 1;
for(int i = 1; i < length1; ++i)
{
output[i] = output[i - 1] * input[i - 1];
}
double temp = 1;
for(int i = length1 - 2; i >= 0; --i)
{
temp *= input[i + 1];
output[i] *= temp;
}
}
}
树中两个结点的最低公共祖先
题目:输入两个树结点,求它们的最低公共祖先。
bool GetNodePath(const TreeNode* pRoot, const TreeNode* pNode, list<const TreeNode*>& path)
{
if(pRoot == pNode)
return true;
path.push_back(pRoot);
bool found = false;
vector<TreeNode*>::const_iterator i = pRoot->m_vChildren.begin();
while(!found && i < pRoot->m_vChildren.end())
{
found = GetNodePath(*i, pNode, path);
++i;
}
if(!found)
path.pop_back();
return found;
}
const TreeNode* GetLastCommonNode
(
const list<const TreeNode*>& path1,
const list<const TreeNode*>& path2
)
{
list<const TreeNode*>::const_iterator iterator1 = path1.begin();
list<const TreeNode*>::const_iterator iterator2 = path2.begin();
const TreeNode* pLast = nullptr;
while(iterator1 != path1.end() && iterator2 != path2.end())
{
if(*iterator1 == *iterator2)
pLast = *iterator1;
iterator1++;
iterator2++;
}
return pLast;
}
const TreeNode* GetLastCommonParent(const TreeNode* pRoot, const TreeNode* pNode1, const TreeNode* pNode2)
{
if(pRoot == nullptr || pNode1 == nullptr || pNode2 == nullptr)
return nullptr;
list<const TreeNode*> path1;
GetNodePath(pRoot, pNode1, path1);
list<const TreeNode*> path2;
GetNodePath(pRoot, pNode2, path2);
return GetLastCommonNode(path1, path2);
}