缓存淘汰算法详解
我们通常在设计一个系统的时候,由于数据库的读取速度远小于内存的读取速度,所以为了加快读取速度,会将一部分数据放到内存中,称为缓存。
但是内存容量是有限的,当你要缓存的数据超出容量,就得有部分数据删除,这时候哪些数据删除,哪些数据保留,就是缓存淘汰算法要干的事。
在缓存系统中,常用的缓存淘汰算法包括:
- FIFO
- LFU
- LRU
- ARC
FIFO
First In First Out,即「先进先出」。

FIFO(First In First Out)按照 “先进先出” 的原理淘汰数据。这正好符合队列的特性,所以,数据结构上使用队列 Queue 来实现。
FIFO算法中,将新访问的数据插入队列尾部,当队列满时,淘汰队列头部的数据。
优点:
实现简单
缺点:
无法根据数据的使用频次、时间等维度进行优化,会导致缓存命中率降低。
LFU
Least Frequently Used 最低频率使用淘汰算法,通常被翻译为「最近最不常用」。
核心思想是:最近使用频率高的数据很大概率将会再次被使用。而最近使用频率低的数据,很大概率不会再使用。
做法:把使用频率最小的数据置换出去。这种算法是完全从使用频率的角度去考虑的。

每当缓存被使用的时候( C B A),则将使用频率加 1,当进行淘汰进程的时候,将使用频率最低的数据淘汰( E )。
优点:
提高频繁使用的数据的命中效率
缺点:
某些数据短时间内被重复引用,并且在很长一段时间内不再被访问。由于它的访问频率计数急剧增加,即使它在相当长的一段时间内不会被再次使用,也不会在短时间内被淘汰。这使得其他可能更频繁使用的块更容易被清除。
此外,刚进入缓存的新项可能很快就会再次被删除,因为它们的计数器较低,即使之后可能会频繁使用。
实现
双向链表
对于基础的数据结构,不论是线性表、链表、队列和栈等等,都应该了然于胸。双向链表的添加与删除操作当然也不例外。
在拥有伪头部和伪尾部的双向链表中采用 头插法 添加一个元素的步骤大家应该也很清晰:
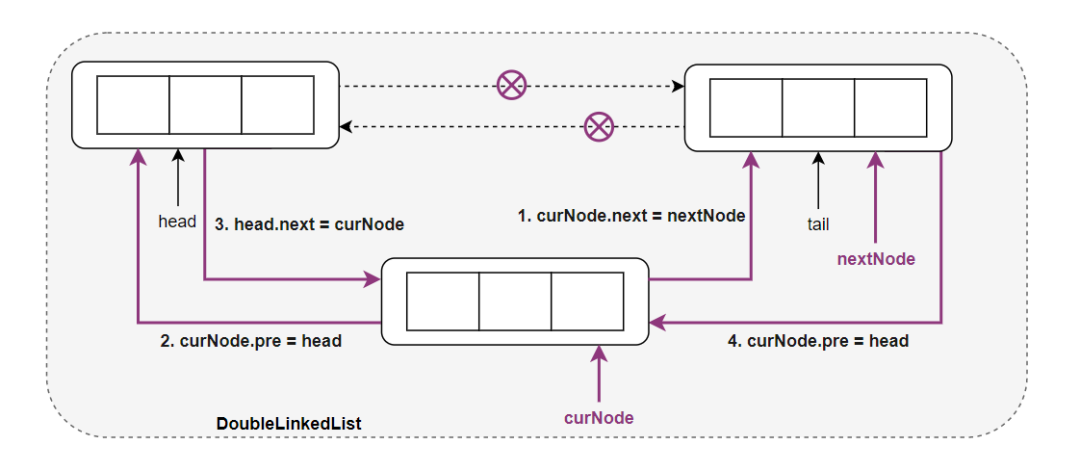
其中 head 指针表示头结点,tail 指针表示尾结点,curNode 表示当前要插入的结点,双向链表插入一个新结点指针的修改顺序一般就是图中的 4 个步骤。
对于删除双向链表尾部结点同样注意结点指针的修改顺序:

其中 curNode 表示当前要删除的结点,preNode 表示当前要删除结点的前驱结点,nextNode 表示当前结点的后继结点,删除双向链表中的一个结点只需将 preNode 的后继结点设置为 nextNode ,而将 nextNode 的前驱结点设置为 preNode 。
哈希
这里你只需掌握一个关键点:利用哈希可以保证我们利用指定的 key 在 O(1)的时间获取到指定的 value ,其中 key 和 value 可以是一个整数值,也可以是一个对象。
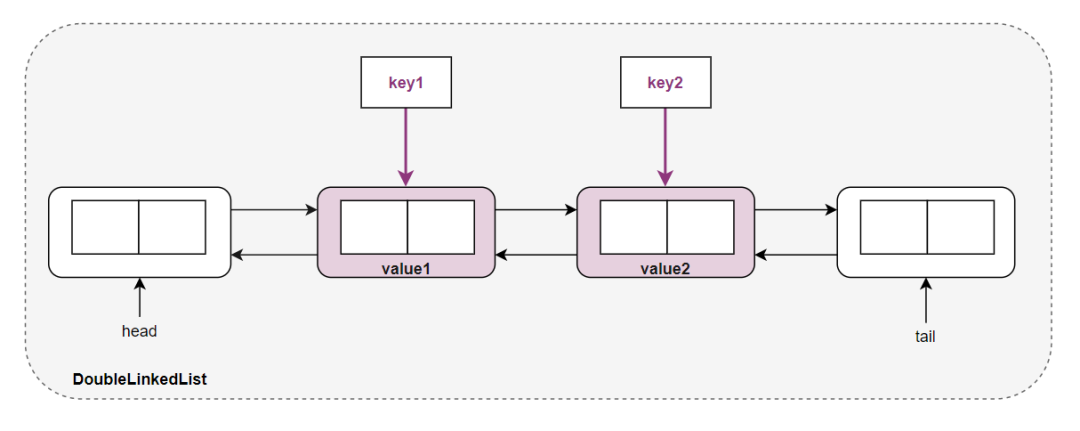
其中的 value 就表示双向链表的一个结点,而 key 则是页号。
双向链表 + 哈希
由于双向链表的查找时间复杂度为 O(n),而插入和删除的复杂度为 O(1) ,要设计一种查找、插入和删除均为 O(1) 的数据结构,哈希算法 + 双向链表便是一个绝妙的组合。
我们可以将双向链表结点和结点的值之间建议一对一的映射关系,便可以在 O(1) 的时间获取到结点本身,然后对结点进行插入和删除操作即可。
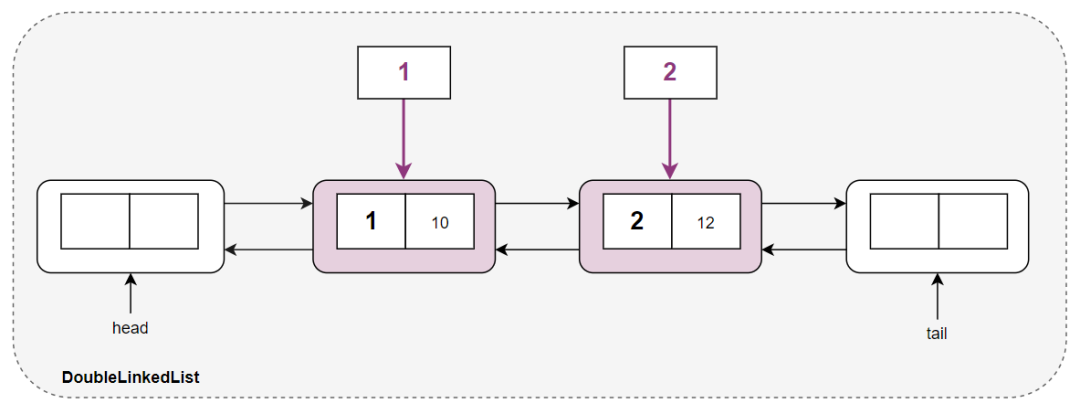
这便是 LRU 和 LFU 的基础框架。
我们也不难写出这样的框架代码:
class Cache {
private Map<Integer, Node> cache;
public int get(int key) {}
public void put(int key, int value) {}
class DoubleLinkedList {}
}
接下来就是完善这个框架。
对于 LFU 算法,涉及到 3 个关键的变量:
-
key ,用来标识一个双向链表的结点;
-
value ,表示 key 所对应的值,也就是结点本身所保存的值;
-
frequency ,表示结点被访问的次数或频度。
有了这三个信息点,我们可以定义出一个双向链表的结点,用来模拟 LFU 的缓存块。
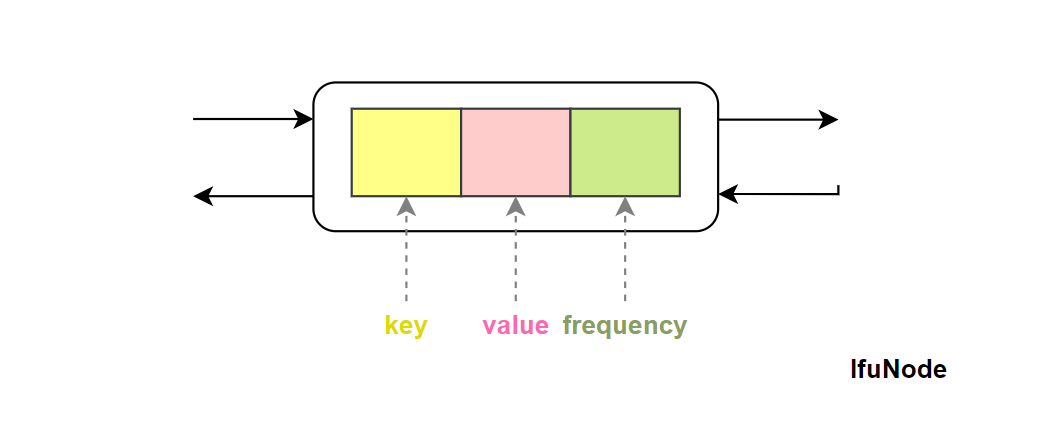
定义一个 LFUNode :
class LFUNode {
int key;
int val;
int frequency;
LFUNode prev;
LFUNode next;
public LFUNode(int key, int val) {
this.key = key;
this.val = val;
this.frequency = 1;
}
}
然后我们可以完善 DoubleLinkedList 类,添加删除和插入的方法:
/**
* listSize 表示双向链表的大小
* head 表示双向链表的头结点
* tail 表示双向链表的尾结点
*/
class DoubleLinkedList {
int listSize;
LFUNode head;
LFUNode tail;
public DoubleLinkedList() {
this.listSize = 0;
this.head = new LFUNode(0, 0);
this.tail = new LFUNode(0, 0);
head.next = tail;
tail.prev = head;
}
/** 在链表的头部添加一个结点,链表长度加 1 **/
public void addNode(LFUNode curNode) {
LFUNode nextNode = head.next;
curNode.next = nextNode;
curNode.prev = head;
head.next = curNode;
nextNode.prev = curNode;
listSize++;
}
/** 删除链表中的结点,链表长度减 1 **/
public void removeNode(LFUNode curNode) {
LFUNode prevNode = curNode.prev;
LFUNode nextNode = curNode.next;
prevNode.next = nextNode;
nextNode.prev = prevNode;
listSize--;
}
/** 删除尾部结点 **/
public LFUNode removeTail() {
// 别忘了判断链表的长度
if (listSize > 0) {
LFUNode tailNode = tail.prev;
removeNode(tailNode);
return tailNode;
}
return null;
}
}
注意 addNode(LFUNode curNode) 方法采用的头插法,将当前结点插入到双向链表的头部;removeTail() 方法删除的双向链表尾部的结点 tail.prev ,一定要注意边界条件的判断,防止操作一块未知的内存空间。
做好准备工作之后,接下来要做的就是设计实现 int get(int key) 和 void put(int key, int value) 两个方法了。
public int get(int key) {
LFUNode curNode = cache.get(key);
if (curNode == null) {
return -1;
}
updateNode(curNode);
return curNode.val;
}
public void put(int key, int value) {
if (cache.containsKey(key)) {
// 更新 key 所对应的值 value
}
else {
// 插入键值对
}
}
其中的 updateNode 表示更新结点的值,具体如何更新我们稍后补充,接下来,我们需要解决的是题目中描述的 “当缓存达到其容量时,则应该在插入新页之前,淘汰最不经常使用的页。在此问题中,当存在平局(即两个或更多个键具有相同使用频率)时,应该去除 最近最久未使用 的键。” 的问题。
当缓存达到其容量时,则应该插入新页之前,淘汰最不经常使用的页。所以我们需要一个全局变量来标识 LRU Cache 的容量,还需要一个标识当前 LFU Cache 当前容量的变量,“淘汰最不经常使用的页” 意味着我们要标识当前 LFU Cache 中访问频率(次数)最少的页面,同时由于不论是访问次数最少的页面,还是其他页面均存在平局的可能,所以我们需要将这些访问频次相同的页面通过双向链表组织在一起,也就是位于同一双向链表中的页面具有相同的频度 freq 。如何快速的访问到某一频度 freq 所对应的双向链表呢?我们就可以考虑将页面的访问次数 freq 与双向链表之间建议映射关系,即利用哈希,在 O(1) 的时间访问到具有相同 freq 的页。
而在具有相同 freq 的双向链表内部,我们通过 LRU 的方法进行处理即可。LFU cache 的数据结构逻辑图就是如下这样:
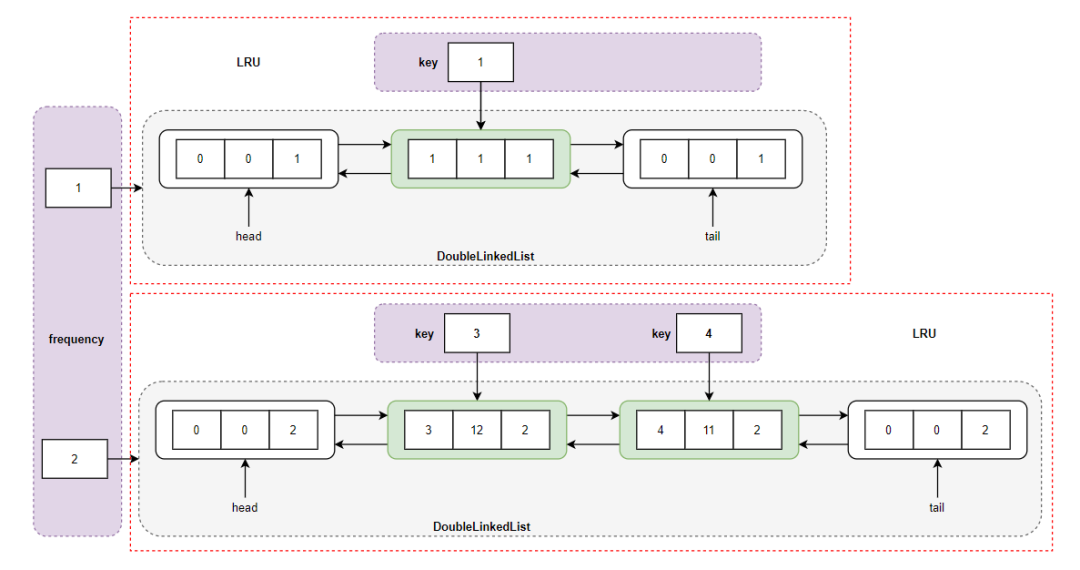
对于这个图的理解,可以让你彻底搞清楚 LRU 和 LFU 的关系,LFU 包含多个 LRU ,其中的红色虚线方框内的结构就是 LRU 数据结构图。
class LFUCache {
private final int capacity; // LFU Cache 的容量
private int curSize; // LFU Cache 当前的容量
Map<Integer LFUNode> cache;
Map<Integer DoubleLinkedList> frequencyMap; // freq 到 DoubleLinkedList 之间的映射关系
public LFUCache(int capacity) {
this.capacity = capacity;
this.curSize = 0;
this.minFrequency = 0;
this.cache = new HashMap<>();
this.frequencyMap = new HashMap<>();
}
}
我们继续完善 put(int key, int value) 方法,要插入键值对,又可以分为两个子条件判断:
-
LFU Cache 的空间已满,在 freq 最小的双向链表内删除最近最少访问的页面(也就是双向链表尾部结点),然后再添加新结点;
-
如果空间足够,则直接添加新结点即可。
public void put(int key, int value) {
if (cache.containsKey(key)) {
LFUNode curNode = cache.get(key);
curNode.val = value;
updateNode(curNode); //更新当前结点的频度
}
else {
curSize++;
if (curSize > capacity) { // LFU Cache 已满
// 获取到访问次数最少的双链表
DoubleLinkedList minFreqList = frequencyMap.get(minFrequency);
LFUNode deleteNode = minFreqList.removeTail(); // 删除 LRU 页面
cache.remove(deleteNode.key); // 在 cache 中删除结点
curSize--;
}
// 因为插入新的结点,所以将最小的访问次数重置为 1
minFrequency = 1; // 插入新的键值对<key, value>
LFUNode newNode = new LFUNode(key, value);
// 获取 freq = 1 所对应的双向链表,如果不存在就新建一个双链表
DoubleLinkedList curList = frequencyMap.getOrDefault(1, new DoubleLinkedList());
curList.addNode(newNode); // 插入新结点
frequencyMap.put(1, curList); // frequency 中添加 1 -> DoubleLinkedList
cache.put(key, newNode); // cache 中添加 key -> newNode
}
}
但是一定要注意在 put() 方法内部最开始对 LFU 的 capacity 进行校验,防止初始化时 LFU 的缓存大小是 0 的情况,直接退出。
public void put(int key, int value) {
if (capacity == 0){
return;
}
}
接下来就是完善最关键的一个方法 updateNode() 方法,该方法出现在两处。
一处是 get(int key) 方法中,用于更新 LFU 缓存当中已存在 key 所对应的 freq ,因为每调用一次 get() 方法,就相当于访问 key 一次,那么该 key 所对应的频率(访问次数)也需要相应的进行更新。
一处出现在 put(int key, int value) 当中,当 key 已经在内存中存在时,则更新 key 所对应的结点 value 以及频率 freq ,同时对 LFU Cache 的存储结构做出调整。
public void updateNode(LFUNode curNode) {
int curFreq = curNode.frequency;
DoubleLinkedList curList = frequencyMap.get(curFreq);
curList.remove(curNode);
// 当前结点的频率 + 1
curNode.frequency++;
// 将频率加 1 之后的结点添加 freq 为 cur.frequency 的新的双向链表中
// 如果该链表不存在,则创建一个新的双向链表并添加 curNode
DoubleLinkedList newList = frequencyMap.getOrDefault(curNode.frequency, new DoubleLinkedList());
newList.addNode(curNode);
frequencyMap.put(curNode.frequency, newList);
}
但上面的这段代码并不完整,因为我们缺少一个关键的边界判断,那就是当前被更新的结点 curNode 刚好在 minFrequency 所指向的双向链表当中,且该双链表中仅包含 curNode 一个结点,从 curList 中删除结点 curNode 将导致整个 LFU 缓存中最少访问次数的提升,即最少访问次数 minFrequency 需要进行加 1 操作 。这一边界情况的判断一定要添加到更新操作之前:
public void updateNode(LFUNode curNode) {
int curFreq = curNode.frequency;
DoubleLinkedList curList = frequencyMap.get(curFreq);
curList.remove(curNode);
// curNode所在双链表的频率为minFrequency 且仅包含 curNode 一个结点
if (curFreq == minFrequency && curList.listSize == 0) {
minFrequency++;
}
// 当前结点的频率 + 1
curNode.frequency++;
// 将频率加 1 之后的结点添加 freq 为 cur.frequency 的新的双向链表中
// 如果该链表不存在,则创建一个新的双向链表并添加 curNode
DoubleLinkedList newList = frequencyMap.getOrDefault(curNode.frequency, new DoubleLinkedList());
newList.addNode(curNode);
frequencyMap.put(curNode.frequency, newList);
}
至此,我们完成了整个 LFU Cache 块的设计和开发。
为了消除你对上面所讲的 LFU 算法的所有疑惑,我们一起以一个简单的例子再作为解释。
图解 LFU
输入:
["LFUCache", "put", "put", "get", "put", "get", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [3], [4, 4], [1], [3], [4]]
输出:
[null, null, null, 1, null, -1, 3, null, -1, 3, 4]
我们对此输入依次进行图解。
LFUCache lfuCache = new LFUCache(2) 表示申请一个容量为 2 的 LFU 缓存。
紧接着执行 put(1,1) 操作,创建一个新的双向链表,并采用头插法插入新的结点 <1,1,1> ,cache 增加到结点的映射,frequencyMap 增加 freq 到双向链表的映射:

执行 put(2,2) 操作,发现 LFU 缓存未满且不包含 key = 2 的结点,而且频率 freq = 1 的双向链表已经存在了,则直接采用头插法将结点 <2,2,1> 插入到频度 freq = 1 所对应的双向链表中:
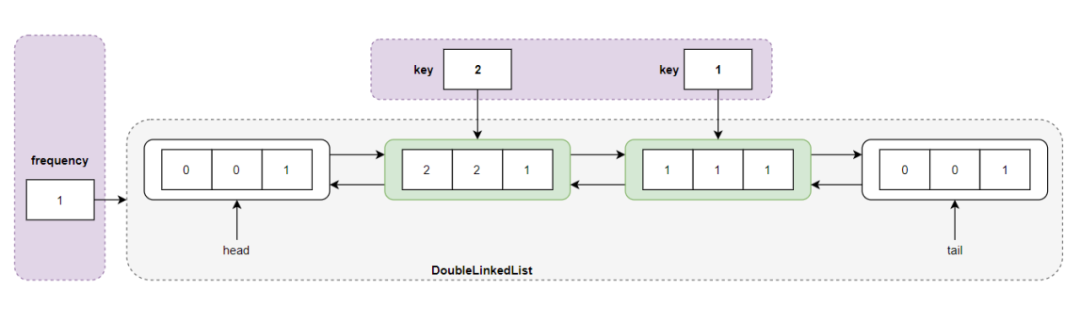
执行 get(1) 操作,发现 key = 1 的结点在 LFU 缓存中,通过 cache 查找到结点,然后调用 updateNode() 函数对结点进行更新,将其频度进行加 1 操作,即结点变成了 <1,1,2> ,但是频度为 2 的链表并不存在,所以创建新链表并插入结点 <1, 1, 2> :
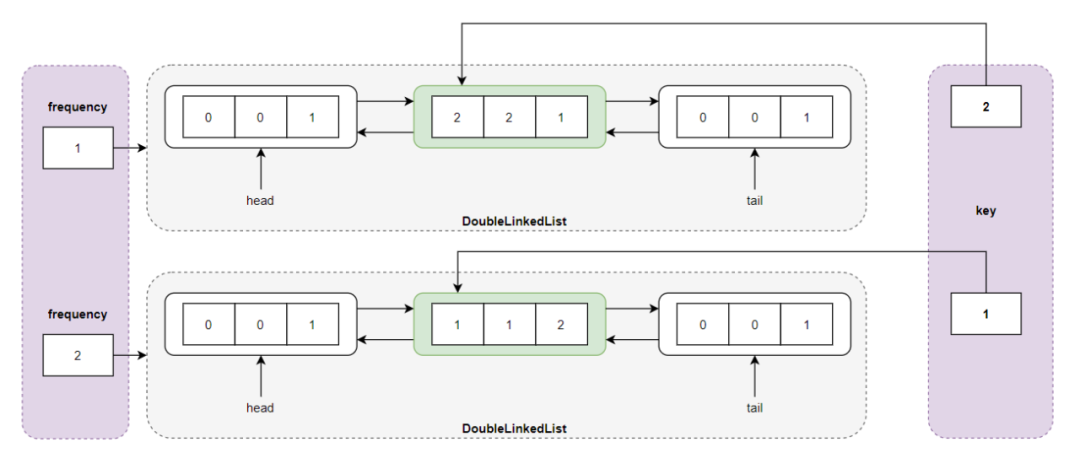
执行 put(3,3) 操作,此时 LFU Cache 的缓存已满 capacity = 2 ,首先删除访问频度最小的双链表中的尾结点 <2,2,1> ,然后插入频度为 1 的新结点 <3,3,1> :

之后执行 get(2) ,key = 2 的结点已经不在 LFU 缓存中了,直接返回 -1 。
执行 get(3) ,返回结点 <3,3,1> 的值 value = 3 ,同时更新结点的频度,这个比较特殊,一定要注意,从频度 frequency = 1 所对应的双向链表中删除结点 <3,3,1> ,然后将结点的频度更新为 2,即 <3,3,2>;但是一定要注意此时频度 frequency = 1 所对应的双向链表中没有结点,也就是说此时最小频度 minFrequency 变成了 2 ,然后将结点 <3,3,2> 插入到频度 freqeuncy = 2 所指向的双向链表的头结点中:
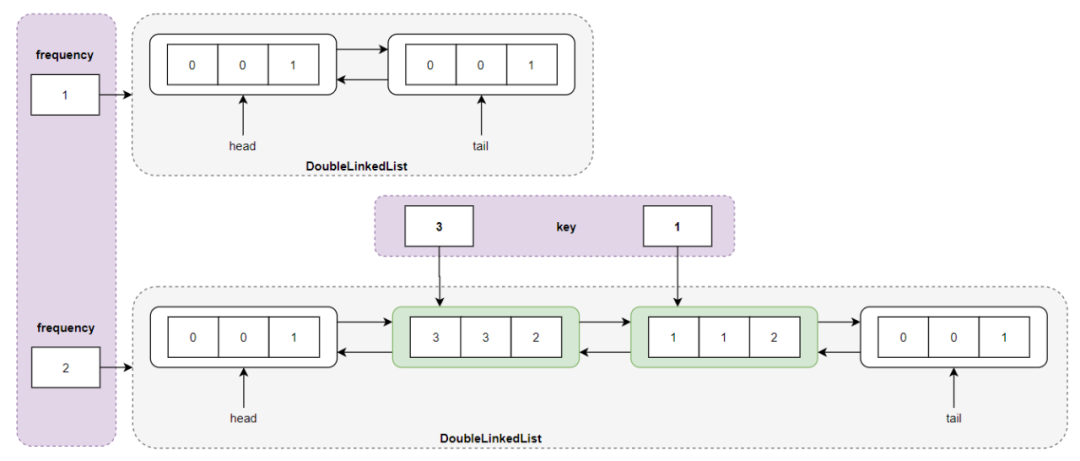
执行 put(4,4) ,发现 LFU Cache 已满,删除频率最小(minFrequency=2)所指向的双向链表的尾结点 <1,1,2> ,然后插入新结点 <4,4,1> ,最小频度变成了 1,即 minFrequency = 1 :
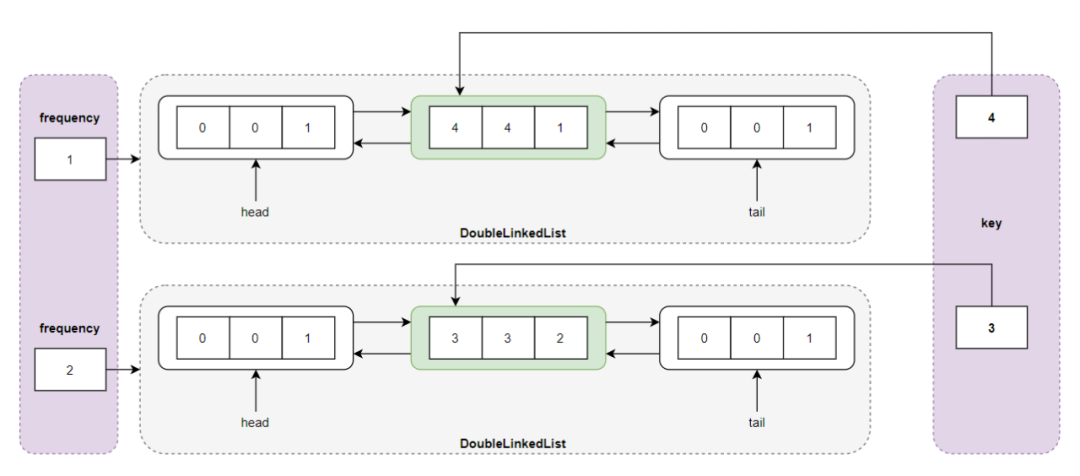
执行 get(1) ,返回 -1,因为前一步我们删除了结点 <1,1,2> 。
然后执行 get(3) 操作,返回 3,但是此时需要更新 key = 3 所对应的结点的频度,首先将结点 <3,3,2>从频度 frequency = 2 所对应的双向链表中删除,并更新结点的频度,将其插入频度 frequency = 3 所对应的双向链表中,注意 frequency = 2 所对应的单链表中没有结点,但这并不影响 LFU Cache 的机制和存储结构,接下来不论是 put() 还是 get() 操作,都会保证我们设计的算法的正确性:

执行 get(4) 操作之后,返回 4 ,更新结点 <4,4,1> ,将 key = 4 所指向的结点 <4,4,1> 从 frequency = 1 所指向的双向链表中删除,然后更新其频度 <4,4,2> ,并将其插入 frequency = 2 所指向的双向链表的头部:

相信看到这里,你已有所悟!完整的实现代码仅供参考:
import java.util.HashMap;
import java.util.Map;
class LFUCache {
private final int capacity;
private int curSize;
private int minFrequency;
private Map<Integer, LFUNode> cache;
private Map<Integer, DoubleLinkedList> frequencyMap;
/*
* @param capacity: LFU Cache 总容量
* @param curSize: LFU cache 当前容量
* @param minFrequency: 全局最小的频度
* @param cache: 保证 O(1) 的时间访问到结点,key-->LFUNode 的映射
* @param frequencyMap: 保证 O(1) 的时间访问到频率为 freq 的结点所对应的双链表
* */
public LFUCache(int capacity) {
this.capacity = capacity;
this.curSize = 0;
this.minFrequency = 0;
this.cache = new HashMap<>();
this.frequencyMap = new HashMap<>();
}
public int get(int key) {
LFUNode curNode = cache.get(key);
if (curNode == null) {
return -1;
}
updateNode(curNode);
return curNode.val;
}
public void put(int key, int value) {
// 边界条件,检查 LFU capacity
if (capacity == 0) {
return;
}
if (cache.containsKey(key)) {
LFUNode curNode = cache.get(key);
curNode.val = value;
updateNode(curNode);
}
else {
curSize++;
if (curSize > capacity) {
// 获取最小频率所对应的双向链表
DoubleLinkedList minFreqList = frequencyMap.get(minFrequency);
LFUNode deleteNode = minFreqList.removeTail();
cache.remove(deleteNode.key);
curSize--;
}
// 重置最小频率,插入新结点
minFrequency = 1;
LFUNode newNode = new LFUNode(key, value);
// 获取到频率为 1 的双向链表并插入新结点
DoubleLinkedList curList = frequencyMap.getOrDefault(1, new DoubleLinkedList());
curList.addNode(newNode);
frequencyMap.put(1, curList);
cache.put(key, newNode);
}
}
public void updateNode(LFUNode curNode) {
int curFreq = curNode.frequency;
DoubleLinkedList curList = frequencyMap.get(curFreq);
curList.removeNode(curNode);
// 防止删除结点所在的频度最小的双向链表仅包含删除结点一个结点
if (curFreq == minFrequency && curList.listSize == 0) {
minFrequency++;
}
curNode.frequency++;
DoubleLinkedList newList = frequencyMap.getOrDefault(curNode.frequency, new DoubleLinkedList());
newList.addNode(curNode);
frequencyMap.put(curNode.frequency, newList);
}
class LFUNode {
int key;
int val;
int frequency;
LFUNode prev;
LFUNode next;
public LFUNode(int key, int val) {
this.key = key;
this.val = val;
this.frequency = 1;
}
}
class DoubleLinkedList {
int listSize;
LFUNode head;
LFUNode tail;
public DoubleLinkedList() {
this.listSize = 0;
this.head = new LFUNode(0, 0);
this.tail = new LFUNode(0, 0);
head.next = tail;
tail.prev = head;
}
// 表头插入一个新结点
public void addNode(LFUNode curNode) {
LFUNode nextNode = head.next;
curNode.next = nextNode;
curNode.prev = head;
head.next = curNode;
nextNode.prev = curNode;
listSize++;
}
// 删除一个结点
public void removeNode(LFUNode curNode) {
LFUNode prevNode = curNode.prev;
LFUNode nextNode = curNode.next;
prevNode.next = nextNode;
nextNode.prev = prevNode;
listSize--;
}
// 删除尾部结点
public LFUNode removeTail() {
// DO NOT FORGET to check list size
if (listSize > 0) {
LFUNode tailNode = tail.prev;
removeNode(tailNode);
return tailNode;
}
return null;
}
}
}
以上的实现方式仅是为了让大家彻底理解 LFU Cache 机制,所以里面的双向链表,以及 key–>LFUNode 的映射,以及 frequency –> DoubleLinkedList 的映射都是我们自己实现的,
LRU
Least Recently used 最近时间未使用,通常被翻译为「最近最少使用」。
核心思想是:最近使用的数据很大概率将会再次被使用。而最近一段时间都没有使用的数据,很大概率不会再使用。
做法:把最长时间未被访问的数据置换出去。这种算法是完全从最近使用的时间角度去考虑的。

B 和 A 都在淘汰进程之前使用过,更新最新的使用时间。 C 则一直没有被使用,虽然不是最久的数据,但是根据 LRU,它需要被淘汰。
最近最少使用页面置换算法,也就是首先淘汰最长时间未被使用的页面。
关键是看页面最后一次被使用到发生调度的时间长短。
优点:
热点数据,可以较长的保存不被淘汰
缺点:
缓存污染:如果某个客户端访问大量历史数据时,可能使缓存中的数据被这些历史数据替换,其他客户端访问数据的命中率大大降低。
实现
LRU 缓存可以看做是哈希表 + 双向链表的特殊数据结构。哈希表使 get() 的时间为 O(1) , 双向链表可以保证结点的添加/删除操作为 O(1)。
我们将一个结点定义如下:
class Node {
int key;
int value;
Node pre;
Node next;
public Node(int key, int value)
{
this.key = key;
this.value = value;
}
}
上面的代码可图形式化表示为:
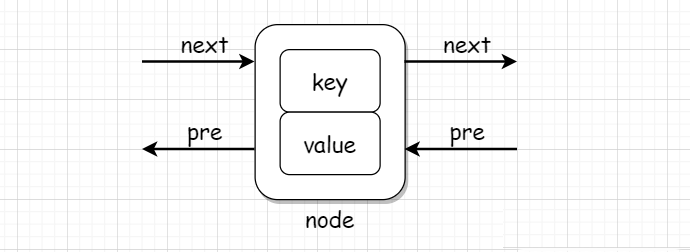
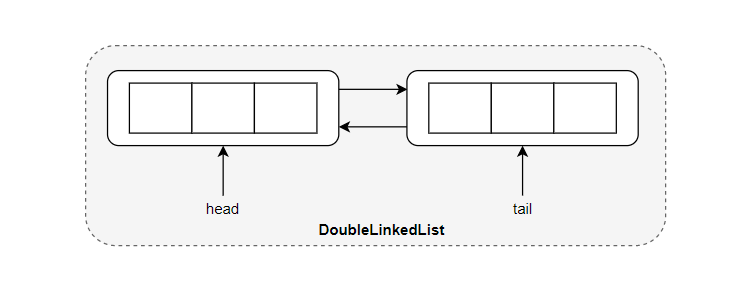
首先我们初始化一个大小为 capacity 的 LRUCache ,其中双向链表使用一个伪头部(dummy head)和伪尾部(dummy tail)标记界限,这样在添加节点和删除节点的时候就不需要检查相邻的节点是否存在。
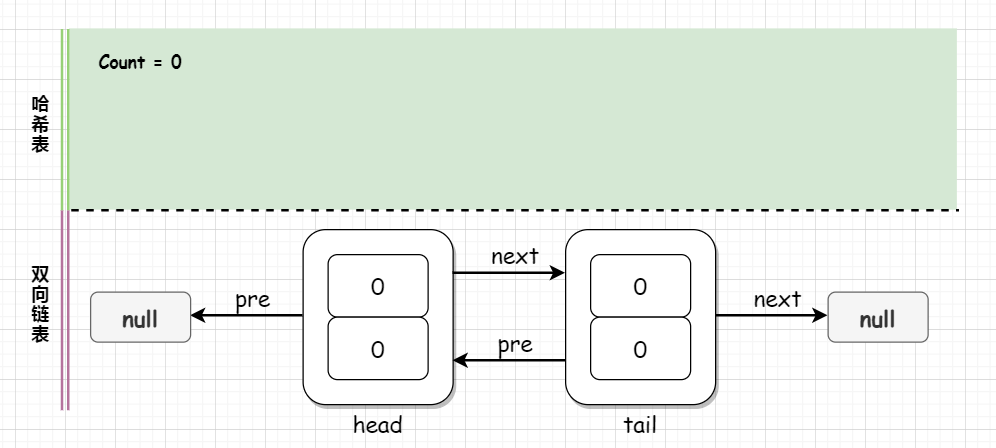
初始化 LRUCache 时,我们同时初始化了一个空的哈希表,从图中暂时还无法看出哈希表和双向链表的结合,我们必然是由哈希表的 key 查找到双向链表中的结点,所以哈希表的值就是双向链表中一个一个的结点。
初始化的代码如下:
public LRUCache(int capacity)
{
this.capicity = capacity; // LRU 缓存大小
map = new HashMap<>(); // 哈希表
head = new Node(0, 0); // dummy head 伪头部
tail = new Node(0, 0); // 伪尾部
head.next = tail;
tail.pre = head;
head.pre = null;
tail.next = null;
count = 0; // 用于记录当前 LRU 缓存中的页面数量
}
执行 void put(int key, int value) ,首先判断哈希表中是否有关键字 key ,如果没有则创建一个新的结点 node ,并在哈希表中添加 <key, node> 键值对,然后判断 LRU 缓存中页面的数量 count 是否小于 LRU 缓存容量 capacity ,如果小于,则直接在头部添加新结点,否则移除哈希表中伪尾部 tail 的前一个结点 tail.pre 所对应的 tail.pre.key ,并在双向链表的头部添加新结点 node ; 如果哈希表中有关键字,则由哈希表获取到该结点,并更新该结点的值,然后删除结点,并将结点添加到双向链表的头部。
执行 lruCache.put(1,10) ,此时 LRU 缓存中页面的数量 (0 = count) < (capacity = 2) LRU 缓存容量,新建一个结点,并将该结点添加到双向链表的头部,同时哈希表中添加一个键值对,key 与结点的 key 相同,而 value 则为其指向的结点,count++ 。我们将双向链表的头部作为最近刚被访问的页面,双向链表的尾部为最近最少使用的页面。

然后执行 lRUCache.put(2, 20); ,此时 LRU 缓存中的页面数量 (1 = count) < (capacity = 2) LRU 缓存容量,与上面的情况一样:
执行 int get(int key) 时,首先判断哈希表中是否有关键字 key ,如果有,则取出关键字 key 所对应的结点 node ,删除 node 结点,然后将 node 结点插入双向链表的头部,并返回 node 结点的值 value ;否则,也就是哈希表中没有找到,则返回 -1 。
执行 int get(1) 时,发现哈希表中有关键字 1 ,首先删除结点 node1 ,然后将 node1 插入到双向链表的头部,并返回 10 。这里的删除和插入操作看似毫无意义,但是这正是 LRU 算法核心思想的一部分,保证最近刚被访问的页面位于双向链表的头部,最近最少访问的页面位于双向链表的尾部,中间的结点有序排列。
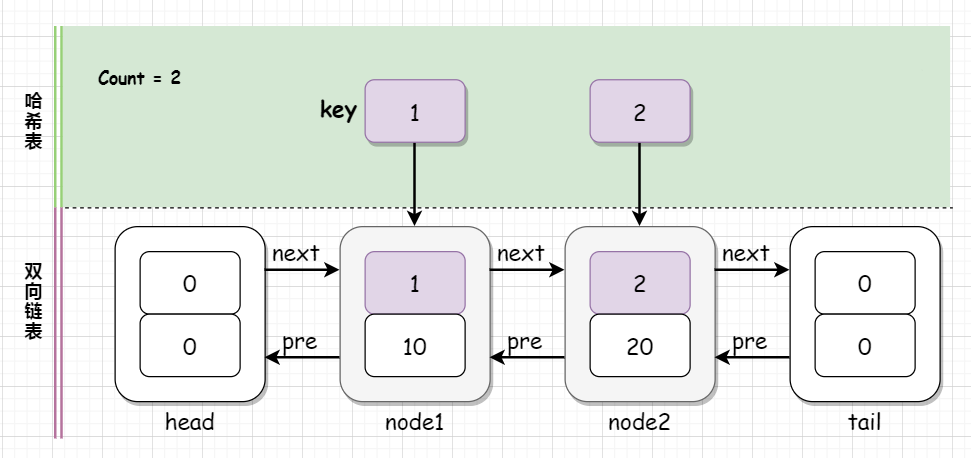
执行 lRUCache.put(3, 30) , 首先没有在哈希表中找到关键 3 ,则创建一个新的结点 node3 ,并将该结点添加到哈希表中,然后判断当前页面容量 count = 2 和 LRU 缓存容量 capacity=2 ,发现 LRU 缓存已满,所以要删除缓存当中最久未被访问的页面(即双向链表的尾部结点 node2),然后在双向链表的头部插入新结点 node3 :

然后执行 lRUCache.get(2) 时,发现哈希表中不存在关键字 2 ,直接返回 -1 。
执行 lRUCache.put(4, 40) ,发现哈希表中不存在关键 4 ,创建新结点 node4 ,并在哈希表中添加 <4, node4> ,然后判断 LRU 缓存是否已满,发现满了,则删除双向链表尾部的元素 node1 ,并将 node4 添加到双向链表的头部。
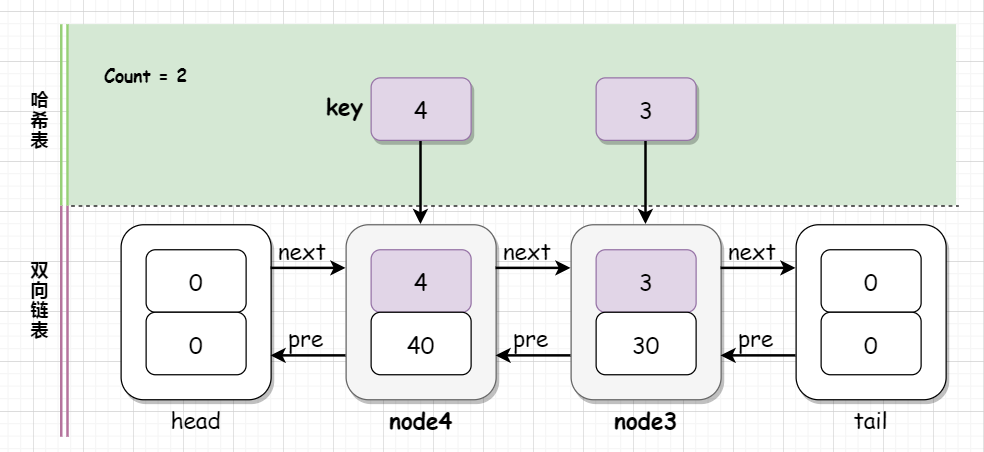
执行 lRUCache.get(1) ,哈希表中未找到关键字 1 ,直接返回 -1 。执行 lRUCache.get(3) ,哈希表中有关键字 3, 获取到关键字所对应的结点 node3 ,然后删除结点 node3 ,再将 node3 插入到双向链表的头部,此时就会看到 node3 和 node4 调换了顺序,返回 30:
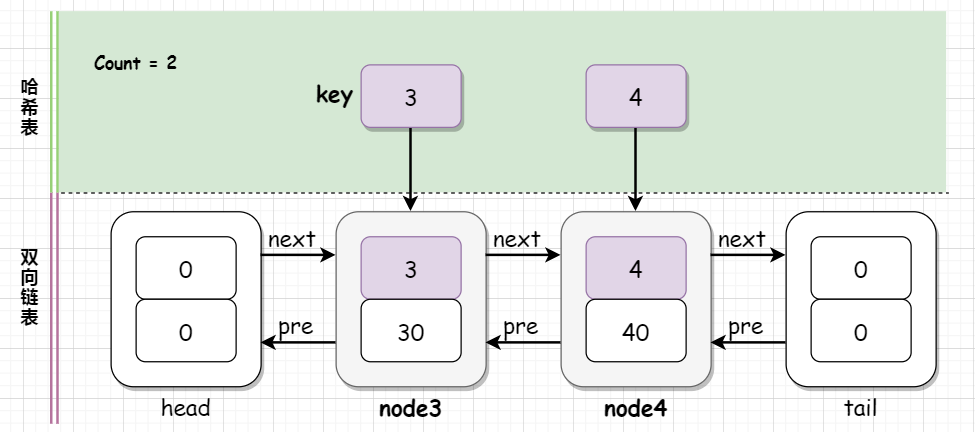
执行 lRUCache.get(4) ,与上面的情况相同,再一次调换 node3 和 node4 在双向链表中的顺序,并返回 40。
我们关注于 LRU 缓存机制的数据结构(哈希表 + 双向链表)本身,而没有详细讲解哈希表和双向链表内部的内容,特别是双向链表的删除和插入操作。LRU 缓存机制的数据结构是集合了哈希表和双向链表两者各自优点的产物,也希望大家看到基础数据结构的重要性。
实现代码如下:
import java.util.HashMap;
// 结点
class Node {
int key;
int value;
Node pre;
Node next;
public Node(int key, int value)
{
this.key = key;
this.value = value;
}
}
// LRU 缓存
class LRUCache {
private HashMap<Integer, Node> map; // 哈希表
private int capacity; // LRU 缓存容量
private int count; // 当前的缓存容量
private Node head, tail; // 伪头部和尾部结点
// 初始化 LRUCache
public LRUCache(int capacity)
{
this.capacity = capacity;
map = new HashMap<>();
head = new Node(0, 0);
tail = new Node(0, 0);
head.next = tail;
tail.pre = head;
head.pre = null;
tail.next = null;
count = 0;
}
// 删除一个结点
public void deleteNode(Node node)
{
node.pre.next = node.next;
node.next.pre = node.pre;
}
// 在双链表的头部添加一个结点
public void addToHead(Node node)
{
node.next = head.next;
node.next.pre = node;
node.pre = head;
head.next = node;
}
// 获取关键字 key 所对应的 value
public int get(int key)
{
if (map.get(key) != null) {
Node node = map.get(key);
int result = node.value;
deleteNode(node);
addToHead(node);
return result;
}
return -1;
}
// 时间复杂度为 O(1)
public void put(int key, int value)
{
if (map.get(key) != null) { // 哈希表中包含关键字 key
Node node = map.get(key); // 获取关键字key所对应的结点 node
node.value = value; // 设置节点的值
deleteNode(node); // 删除结点
addToHead(node); // 将结点插入到头结点
}
else {// 哈希表中不包含关键字 key
Node node = new Node(key, value); // 创建新结点 node
map.put(key, node); // 将结点<key node>添加到哈希表中
if (count < capacity) { // 当前的LRU缓存容量未满
count++;
addToHead(node); // 直接将结点添加到双链表头部
}
else {
map.remove(tail.pre.key); // 哈希表中移除最久未被使用的页面
deleteNode(tail.pre); // 双链表中删除最近最少被使用页面
addToHead(node); // 将新结点添加到双链表头部
}
}
}
}
public class TestLRUCache {
public static void main(String[] args)
{
LRUCache cache = new LRUCache(2);
cache.put(1, 10);
cache.put(2, 20);
System.out.println("Key = 1, value = " +
cache.get(1));
cache.put(3, 30);
System.out.println("Key = 2, Value = " +
cache.get(2));
cache.put(4, 40);
System.out.println("Key = 1, Value = " +
cache.get(1));
System.out.println("Key = 3, Value = " +
cache.get(3));
System.out.println("Key = 4, Value = " +
cache.get(4));
}
}
哈希链表
前面给的方法是 哈希表 + 双向链表 ,其中哈希表使用的是 Java 中的 HashMap ,双向链表英文名为 double Linked List ,两者的结合体就是 Linked Hash Map ,又名 哈希链表 。
Java 中提供了现成的哈希链表,即 LinkedHashMap :
public class LinkedHashMap<K,V> extends HashMap<K,V> implements Map<K,V>{}
基于 LinkedHashMap 的实现代码简直炒鸡简单:
class LRUCache {
private LinkedHashMap<Integer, Integer> map;
private final int CAPACITY;
// 初始化 LRU 缓存
public LRUCache(int capacity)
{
CAPACITY = capacity;
map = new LinkedHashMap<Integer, Integer>(capacity, 0.75f, true) {
protected boolean removeEldestEntry(Map.Entry eldest)
{
return size() > CAPACITY;
}
};
}
// 时间复杂度 O(1)
public int get(int key)
{
return map.getOrDefault(key, -1);
}
// 时间复杂度 O(1)
public void set(int key, int value)
{
map.put(key, value);
}
}
基于哈希链表的实现简单,实则和哈希表 + 双向链表的实现方式一样,我们依次对代码中涉及的几个回调函数和构造方法进行说明。
首先是 LinkedHashMap 的构造函数:
/**
* LinkedHashMap 构造方法
*
* @param initialCapacity 初始容量
* @param loadFactor 装载因子
* @param accessOrder true 访问顺序
* access-order, false 为插入序(默认)
* @throws 如果初始容量为负值或者装载因子为非正值,则抛 IllegalArgumentException
*/
public LinkedHashMap(int initialCapacity,
float loadFactor,
boolean accessOrder) {
super(initialCapacity, loadFactor);
this.accessOrder = accessOrder;
}
其中的 initialCapacity 就是 LRU 缓存的容量 capacity ,装载因子取 0.75f ,也就是默认值,accessOrder 表示哈希链表的排序方式, accessOrder = true 表示按照结点的访问顺序排序,accessOrder = false 表示按照结点的插入顺序排序,默认为 false,但是 LRU 缓存机制显然是按照结点的访问顺序排序的,所以传入 true .
再来看一下我们覆写的方法 removeEldestEntry ,我给大家翻译了源码中的部分注释,我们覆写的代码其实注释中给了,size() > CAPACITY 就表示当 LinkedHashMap 的容量大于 CAPACITY 时,则删除最旧的页面,由于我们的 accessOrder = true 则相当于删除最近最少被访问的结点。
/**
* 如果哈希表要删除其最旧的结点,则返回 true.
* 在哈希表中插入新的结点后,put 和 putAll 方法会调用该方法
* 每次添加新的结点时,该函数为实现者提供了删除旧结点的机会。
* 如果用哈希表表示缓存时,该函数就会非常有用:
* 该函数允许删除旧的结点,从而减少内存消耗。
* 使用示例:覆写该方法,可以保证哈希表在最多可以容纳100个结点的情况下,
* 每次添加新结点时都会删除最旧的结点,从而保持100个结点的稳定状态。
* <pre>
* private static final int MAX_ENTRIES = 100;
*
* protected boolean removeEldestEntry(Map.Entry eldest) {
* return size() > MAX_ENTRIES;
* }
* </pre>
*
* 此方法默认返回值为 false,也就是不会修改哈希表,
* 但是其允许哈希表根据其返回值修改哈希表本身。
* 允许此方法直接修改哈希表,但如果这样做,则必须返回 false
*(指示该哈希表不应尝试任何进一步的修改)。
* 在此方法中修改哈希表后返回true的效果未指定。
* 默认实现仅返回 false;
* 此时 LinkedHashMap 类似于普通的哈希表-永远不会删除最旧的结点)。
* @param eldest:哈希表中最近最少插入(least recently inserted)的结点
* 如果是按访问顺序排序的哈希表,
* eldest 则表示最近最少访问(least recently accessed)的结点。
* 如果该方法返回 true, 则删除该结点.
* @return 如果最旧的结点要删除,返回 true, 否则,返回false。
*/
protected boolean removeEldestEntry(Map.Entry<K,V> eldest) {
return false;
}
getOrDefault 方法的代码更简单,就是哈希链表中有关键字 key ,则返回关键字所对应结点则值,否则返回默认值 -1:
public V getOrDefault(Object key, V defaultValue) {
Node<K,V> e;
if ((e = getNode(hash(key), key)) == null)
return defaultValue;
if (accessOrder)
afterNodeAccess(e);
return e.value;
}
至于添加方法 put(int key, int value) 则是向 LinkedHashMap 中添加结点,内部操作和哈希表 + 双向链表的思想基本一致,但是实现不同:
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
其中 putVal(hash(key), key, value, false, true) 是 HashMap 的方法!
LRU的改进算法
LRU算法中,当某一时间节点,产生了大量仅访问了一次的数据,会造成热点数据的淘汰。为此,可以对 LRU 算法进行改进,对「最近访问页面的次数」进行策略优化。
LRU-K算法
LRU-K算法相对于LRU算法来说多维护了一个队列用来存放访问历史数据,所有新加入缓存的数据都会加入到历史访问队列中,当历史访问队列中数据的访问次数达到K,才会将数据放置到LRU缓存队列中。
LRU算法可以理解为K为1的LRU-K算法,这个算法主要是解决缓存污染的问题,将数据访问一次就进入缓存队列的条件提高到访问K次才能进入缓存队列。
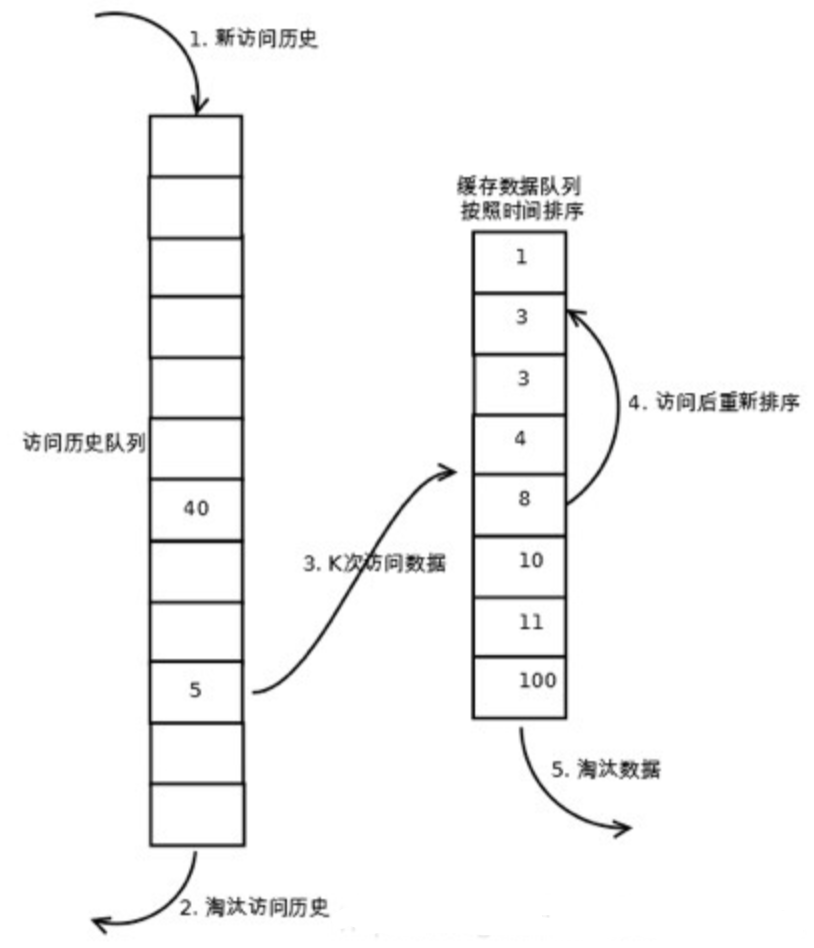
执行过程理解:
1、在LRU缓存队列中查找客户端需要访问的数据。 如果缓存命中,则将访问的数据中队列中取出,重新加入到缓存队列的头部。
2、如果没有命中,表示缓存穿透,从磁盘中获取访问数据,并且判断历史访问队列中是否存在该数据索引。
3、如果历史访问队列中存在该数据索引,则将索引的访问次数加1,否则加入该数据索引;
4、当历史访问队列中的数据访问次数达到K,将数据加入到LRU缓存队列的头部,并从历史访问队列中移除。
5、如果此时LRU缓存队列满了,则需要先置换出去一个数据,淘汰队列尾部的数据,即淘汰“倒数第K次访问离现在最久”的数据。然后再在队列头部加入新数据。
历史访问队列可以按照FIFO或者LRU的规则来管理数据。LRU-K 算法的核心思想就是将访问一次就能淘汰其余缓存的 “1” 提升为 “K”。
优点:
避免了仅访问 1 次就能淘汰其余缓存的 “缓存污染” 问题,提高了缓存命中率。
缺点:
根据K的设置值越大,需要更多次访问才能清空历史访问队列中的数据,但是命中率会更高。相比LRU算法,需要占用的内存更大。
LRU-K具有LRU的优点,同时能够避免LRU的缺点,实际应用中LRU-2是综合各种因素后最优的选择,LRU-3或者更大的K值命中率会高,但适应性差,需要大量的数据访问才能将历史访问记录清除掉。
2Q
Two Queues,简称为 2Q。2Q 算法其实是 LRU-K 的一个具体版本,LRU-2。并且 2Q 算法中的历史队列,采用 FIFO 的方法进行缓存的
当数据第一次访问时,2Q算法将数据缓存在FIFO队列里面,当数据第二次被访问时,则将数据从FIFO队列移到LRU队列里面,两个队列各自按照自己的方法淘汰数据。详细实现如下:
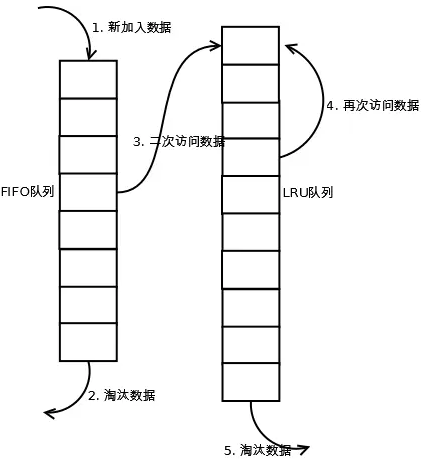
执行过程理解:
1、在LRU缓存队列中查找客户端需要访问的数据。 如果LRU缓存队列中命中,则将访问的数据中队列中取出,重新加入到缓存队列的头部。
2、如果LRU缓存队列中没有命中,在FIFO缓存队列中查找访问数据。
3、如果FIFO缓存队列中命中,将数据加入到LRU缓存队列的头部,并从FIFO缓存队列中移除;
4、如果LRU缓存队列满了,则需要先置换出去一个数据,淘汰队列尾部的数据,然后再在队列头部加入新数据。
5、如果FIFO缓存队列中没有命中,表示缓存穿透,从磁盘中读取该数据,并将数据缓存到FIFO队列中。
6、如果FIFO缓存队列满了,则需要先置换出去一个数据,淘汰队列尾部的数据,即淘汰最先进入队列的数据。然后再在队列头部加入新数据。
优点:
相比LRU-2算法,可以减少一次从磁盘读取数据的操作。
缺点:
相比LRU算法,需要占用的内存更大。
Mysql的变种LRU算法
InnoDB中应用的LRU优化算法:使用链表来实现的。

在 InnoDB 实现上,按照 5:3 的比例把整个 LRU 链表分成了 young 区域和 old 区域。图中 LRU_old 指向的就是 old 区域的第一个位置,是整个链表的 5/8 处。也就是说,靠近链表头部的 5/8 是 young 区域,靠近链表尾部的 3/8 是 old 区域。改进后的 LRU 算法执行流程如上图。
1、在缓存中查询数据。
2、如果命中,如State 1所示,要访问数据页 P3,由于 P3 在 young 区域,因此和优化前的 LRU算法一样,将其移到链表头部,变成状态 2;
3、如果命中,且P3在old区域,则判断数据页在 LRU 链表中存在的时间是否超过了 1秒,如果是就把它移动到链表头部,也就是移到young区域的头部;如果不是,位置保持不变。( 1秒这个时间,是由参数innodb_old_blocks_time 控制的。其默认值是 1000,单位毫秒。)
4、如果没有命中,则淘汰数据页Pm,并将新数据页Px插入到LRU_old链表部分的头部。
5、如果LRU_old链表满了,则淘汰处于链表尾部的数据页。如果LRU_young链表满了,则淘汰处于young区域链表尾部的数据页。
这个策略,就是为了处理类似全表扫描的操作量身定制的。如果大量扫描历史数据表,扫描过程中,新插入的数据页都被放到 old 区域 ;一个数据页里面有多条记录,这个数据页会被多次访问到,但由于是顺序扫描,这个数据页第一次被访问和最后一次被访问的时间间隔不会超过 1 秒,因此还是会被保留在 old 区域;再继续扫描后续的数据,之前的这个数据页之后也不会再被访问到,于是始终没有机会移到链表头部(也就是 young 区域),很快就会被淘汰出去。
这个策略最大的收益,就是在扫描这个大表的过程中,虽然也用到了Buffer Pool,但是对 young 区域完全没有影响,从而保证了Buffer Pool响应正常业务的查询命中率。
ARC
Adaptive Replacement Cache,即「自适应缓存替换」算法,是一种自适应性 Cache 算法, 它结合了 LRU 与 LFU。
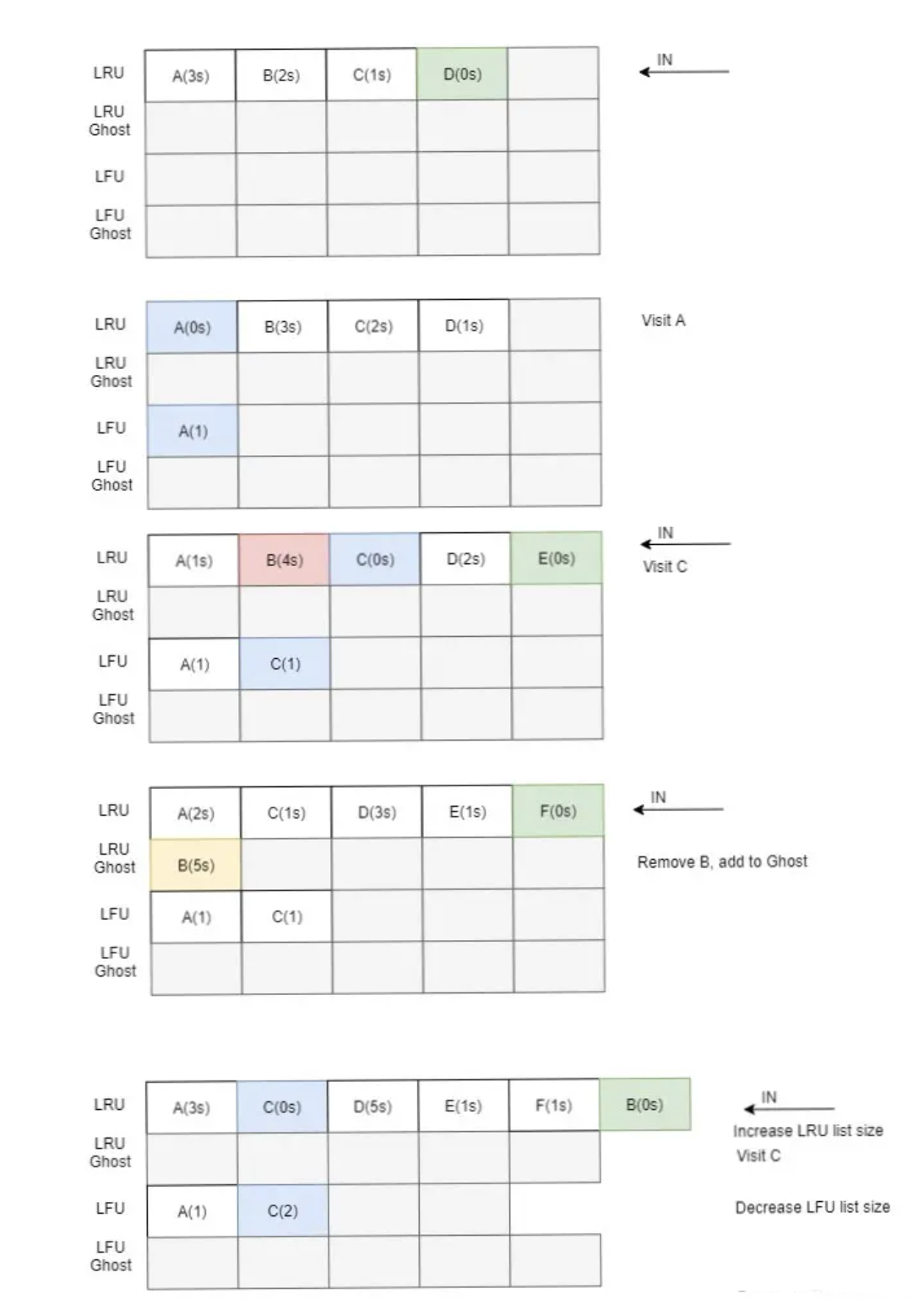
ARC 的精髓就是根据被淘汰数据的访问情况,而增加对应 LRU 还是 LFU 链表的大小。
ARC 包含了四个链表:
-
最近最多使用的页面链表 (LRU list)
-
最近最频繁使用的页面链表(LFU list)
-
存储那些最近从最近最多使用链表中淘汰的页面信息(Ghost list for LRU)
-
存储那些最近从最近最频繁使用链表中淘汰的页面信息(Ghost list for LFU)
ghost链表不储存数据(仅仅储存页面信息,比如offset,dev-id)
当数据 A 加入 LRU 后,如果 A 再次被访问,则同时被放到 LFU 链表中。所以 LFU 链表的缓存为 LRU 链表的多次访问的数据。
当 LRU 链表淘汰了 B,那么 B 的信息则进入到 LRU Ghost 链表。如果 B 在之后再次被访问,则增加 LRU 链表的大小,同时缩减 LFU 链表的大小。LFU 链表同理。
也就是说,利用这种适应机制,当系统趋向于访问最近的内容,会更多地命中LRU ghost list,这样会增大LRU的空间; 当系统趋向于访问最频繁的内容,会更多地命中LFU ghost list,这样会增加LFU的空间.
优点:
可以根据被淘汰数据的访问情况,自适应地动态地增加 LRU 或 LFU 链表的大小。
缺点:
占用内存较多
总结
每一种算法都有自己的特色,但是真正用在程序中,或多或少都会进行对应的优化。比如 Redis 会同时使用 LRU 和 LFU ,同时 LFU为了体现时间维度特征而会主动将计数器减少等策略。