js 数字类型精度问题
话题研究的背景
今天在计算商品价格的时候再次遇到 js 浮点数计算出现误差的问题,以前就一直碰到这个问题,都是简单的使用 tofixed 方法进行处理一下,这对于一个程序员来说是及其不严谨的。所以今天查阅资料对 js 数字类型精度问题做个总结。
我们先来看一段 JS。
console.log( 0.1+ 0.2); // 0.30000000000000004
console.log( 0.1+ 0.2 == 0.3); // false
是不是很奇葩,其实对于浮点数的四则运算,几乎所有的编程语言都会有类似精度误差的问题,只不过在 C++/C#/Java 这些语言中已经封装好了方法来避免精度的问题,而 JavaScript 是一门弱类型的语言,从设计思想上就没有对浮点数有个严格的数据类型(数字其实都是浮点类型),所以精度误差的问题就显得格外突出。下面就分析下为什么会有这个精度误差,以及怎样修复这个误差。
双精度浮点数表示法
JavaScript 数字采用的是 IEEE-754 标准的双精度浮点数表示法,也就是说在 js 中不管是整数还是小数都是双精度浮点类型,也就是其他语言中的 double 类型。
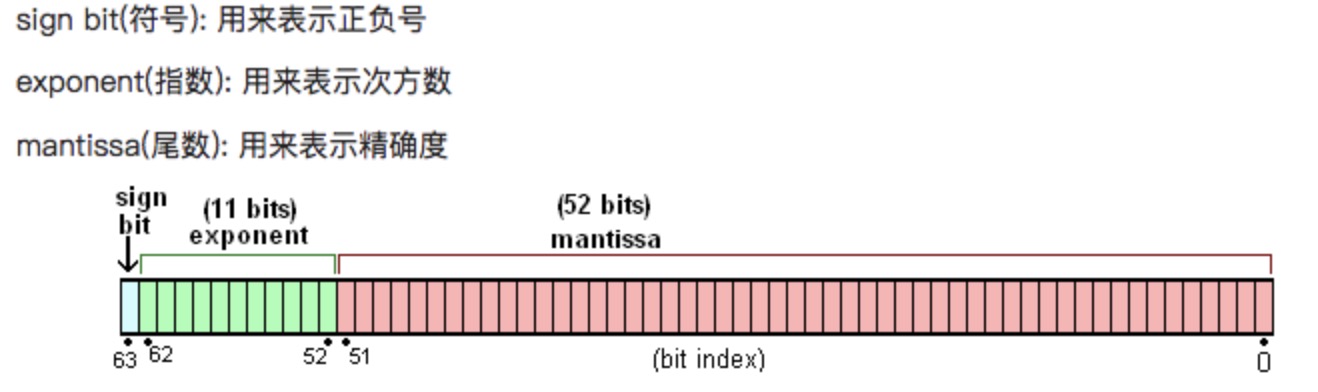
一个 Number 类型的数字在内存中会被表示成:s x m x 2^e这样的格式。 在 ES 规范中规定 e 的范围在-1074 ~ 971(这里注意并不是(2^11)/2),而 m 最大能表示的最大数是 52 个 1,最小能表示的是 1,这里需要注意:
二进制的第一位有效数字必定是 1,因此这个 1 不会被存储,可以节省一个存储位,因此尾数部分可以存储的范围是 1 ~ 2^(52+1)。
也就是说 Number 能表示的最大数字绝对值范围是 2^-1074 ~ (2^53 - 1)*(2^971),能够准确表示的整数范围在 -2^53 到 2^53 之间(不含两个端点),超过这个范围就无法精确表示,我们验证如下:
JS中能否表示的数字的绝对值范围:
Number.MAX_VALUE // 1.7976931348623157e+308
Number.MIN_VALUE // 5e-324
(2**53 -1)*(2**971) // 1.7976931348623157e+308
2**(-1074) // 5e-324
JS中能够表示的最大安全整数的范围:
Number.MAX_SAFE_INTEGER // 9007199254740991
Number.MIN_SAFE_INTEGER // -9007199254740991
2**53 -1 // 9007199254740991
-(2**53 -1) // -9007199254740991
精度丢失
前面提到,计算机中存储小数是先转换成二进制进行存储的,我们来看一下 0.1 和 0.2 转换成二进制的结果:
(0.1)10 => (0.00011001100110011001(1001)...)2
(0.2)10 => (0.00110011001100110011(0011)...)2
可以发现,0.1 和 0.2 转成二进制之后都是一个无限循环的数,前面提到尾数位只能存储最多 53 位有效数字,这时候就必须来进行四舍五入了,而这个取舍的规则就是在 IEEE 754 中定义的,最终能被存储的有效数字是:
0.0001(1001)(1001)(1001)(1001)(1001)(1001)(1001)(1001)(1001)(1001)(1001)(1001)101
+
0.(0011)(0011)(0011)(0011)(0011)(0011)(0011)(0011)(0011)(0011)(0011)(0011)(0011)01
=
0.0100(1100)(1100)(1100)(1100)(1100)(1100)(1100)(1100)(1100)(1100)(1100)(1100)111
这里注意,53 位的存储位指的是能存 53 位有效数字,因此前置的 0 不算,要往后再取到 53 位有效数字为止。
最终的这个二进制数转成十进制就是 0.30000000000000004(不信的话可以找一个在线进制转换工具试一下。
到此,这个精度丢失的问题已经解释清楚了,用一句话来概括就是,计算机中用二进制来存储小数,而大部分小数转成二进制之后都是无限循环的值,因此存在取舍问题,也就是精度丢失。
最大安全整数
最大安全整数 9007199254740991 对应的二进制数如图:

53 位有效数字都存储满了之后,想要表示更大的数字,就只能往指数数加一位,这时候尾数因为没有多余的存储空间,因此只能补 0。
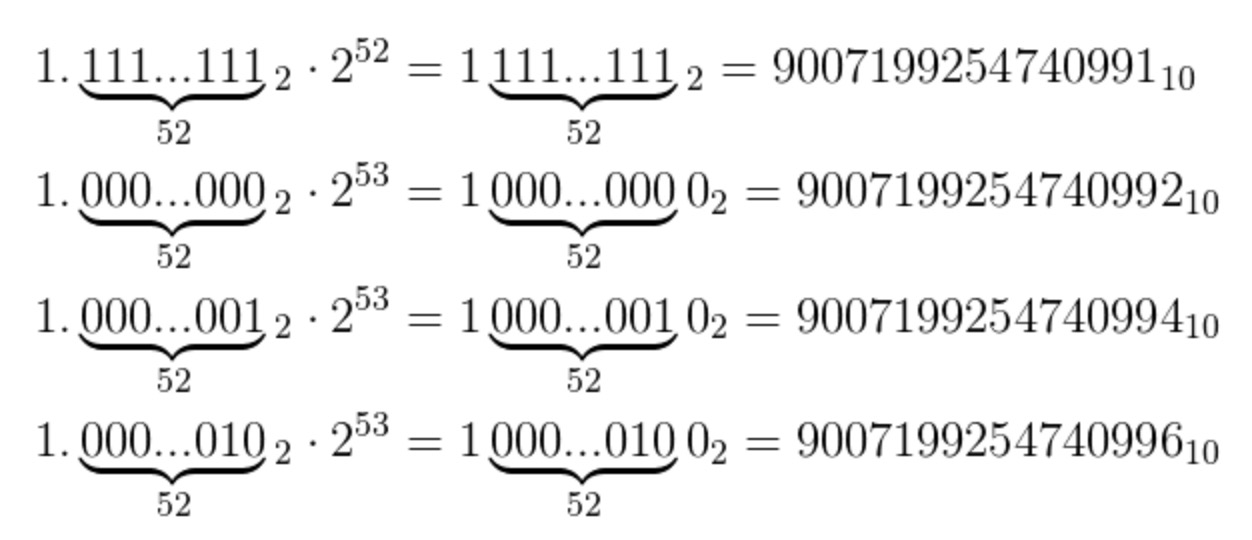
这里注意,尾数部分会进行规范化,比如 0.1 的二进制是 0.00011001100110011001(1001) x 2^0,规范化(就是控制尾数在 1-2 之间)后是 1.1001100110011001(1001) x 2^-4,此时指数位是 -4,尾数是去掉前面 1. 之后的部分,这就是 0.1 在双精度下的表示。
在指数位为 53 的情况下,最后一位尾数位为 0 的数字可以被精确表示,而最后一位尾数为为 1 的数字都不能被精确表示。也就是可以被精确表示和不能被精确表示的比例是 1:1。
同理,当指数为 54 的时候,只有最后两位尾数为 00 的可以被精确表示,也就是可以被精确表示和不能被精确表示的比例是 1:3,当有效位数达到 x(x>53)的时候,可以被精确表示和不能被精确表示的比例将是 1 : 2^(x-53) - 1。
可以预见的是,在指数越来越高的时候,这个指数会成指数增长,因此在 Number.MAX_SAFE_INTEGER ~ Number.MAX_VALUE 之间可以被精确表示的整数可以说是凤毛麟角。
之所以会有最大安全整数这个概念,本质上还是因为数字类型在计算机中的存储结构。在尾数位不够补零之后,只要是多余的尾数为 1 所对应的整数都不能被精确表示。
Number.prototype.toFixed()
toFixed() 方法使用定点数表示法来格式化一个数字,返回值为 String 类型。值得注意的是该方法的舍入法则并不是四舍五入,很多人对此有误解。而且,不同浏览器对 toFixed() 方法的处理结果是不同的。比如:(2.445).toFixed(2) 在 IE 中的执行结果为 “2.45”,但是在 Chrome 中的执行结果为 “2.44”。曾经某商城出现不同浏览器上显示价格不一样的问题就是使用了 toFixed() 方法导致的。总的来说,toFixed() 方法不能用来处理这种小数舍入问题。
Math.round() 方法的问题
Math.round() 函数返回一个数字四舍五入后最接近的整数。不同于 toFixed() 方法,Math.round() 方法本身没有问题,你可以放心的使用它对一个数字进行四舍五入。但是实际场景中,我们往往需要处理的是计算结果而非字面量。问题就出在这个计算上,比如 2.445 \* 100 的计算结果不是 244.5 而是 244.49999999999997,这个时候再使用 Math.round() 方法,其结果自然和预期的不一样了。
Math.round(244.5) // 245
Math.round(2.445 * 100) // 244
2.445 * 100 === 244.5 // false
总结
可以发现,不管是浮点数计算的计算结果错误和大整数的计算结果错误,最终都可以归结到 JS 的精度只有 53 位(尾数只能存储 53 位的有效数字)。那么我们在日常工作中碰到这两个问题该如何解决呢?
大而全的解决方案就是使用 mathjs,看一下 mathjs 的输出:
math.config({
number: 'BigNumber',
precision: 64
});
console.log(math.format(math.eval('0.1 + 0.2'))); // '0.3'
console.log(math.format(math.eval('0.23 * 0.34 * 0.92'))); // '0.071944'
console.log(math.format(math.eval('9007199254740991 + 2'))); // '9.007199254740993e+15'
其实平时在遇到整型溢出的情况是非常少的,大部分场景是浮点数的计算,如果不想因为一些简单的计算引入 mathjs 的话,也可以自己来实现运算函数,这里一般是把需要计算的数字乘以 10 的 n 次幂,换算成计算机能够精确识别的整数,然后再除以 10 的 n 次幂。
大部分编程语言都是这样处理精度差异的(需要考虑数字是否越界和当数字被表示成科学计数法的场景),如果懒得自己实现的话,可以使用这个 1k 都不到的 number-precision,这个工具库 API 简洁很多,已经可以解决浮点数的计算问题了(看了代码,对于超出 Number.MAX_SAFE_INTEGER 的数字的处理方式是抛出 warning)。